Understanding Generalization of Deep Neural Networks Trained with Noisy Labels

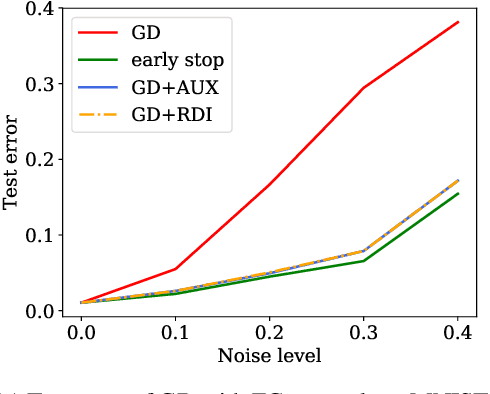
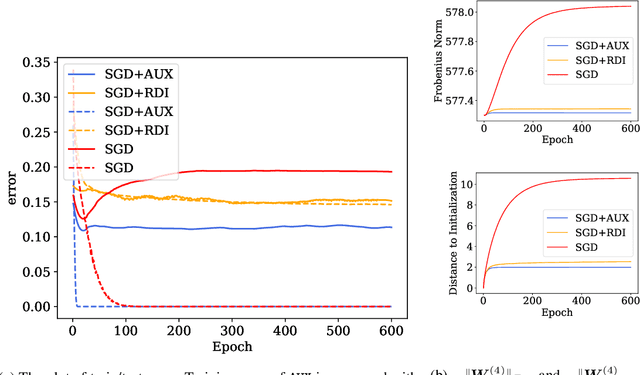
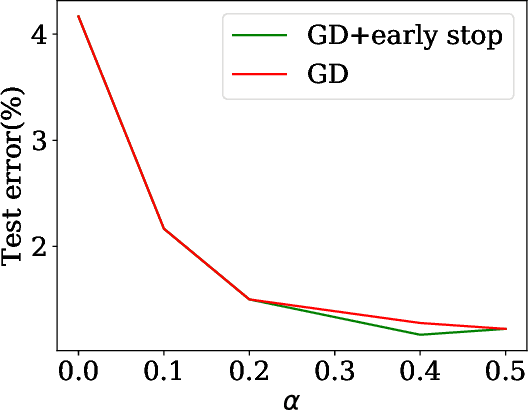
Over-parameterized deep neural networks trained by simple first-order methods are known to be able to fit any labeling of data. Such over-fitting ability hinders generalization when mislabeled training examples are present. On the other hand, simple regularization methods like early-stopping seem to help generalization a lot in these scenarios. This paper makes progress towards theoretically explaining generalization of over-parameterized deep neural networks trained with noisy labels. Two simple regularization methods are analyzed: (i) regularization by the distance between the network parameters to initialization, and (ii) adding a trainable auxiliary variable to the network output for each training example. Theoretically, we prove that gradient descent training with either of these two methods leads to a generalization guarantee on the true data distribution despite being trained using noisy labels. The generalization bound is independent of the network size, and is comparable to the bound one can get when there is no label noise. Empirical results verify the effectiveness of these methods on noisily labeled datasets.