Toward a unified theory of sparse dimensionality reduction in Euclidean space
Paper and Code
Aug 25, 2015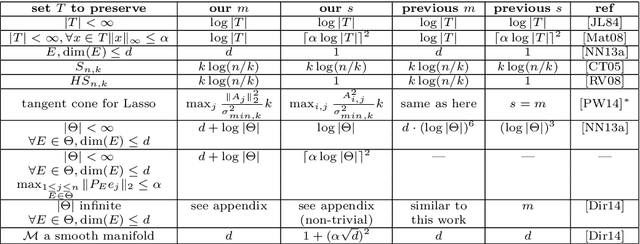
Let $\Phi\in\mathbb{R}^{m\times n}$ be a sparse Johnson-Lindenstrauss transform [KN14] with $s$ non-zeroes per column. For a subset $T$ of the unit sphere, $\varepsilon\in(0,1/2)$ given, we study settings for $m,s$ required to ensure $$ \mathop{\mathbb{E}}_\Phi \sup_{x\in T} \left|\|\Phi x\|_2^2 - 1 \right| < \varepsilon , $$ i.e. so that $\Phi$ preserves the norm of every $x\in T$ simultaneously and multiplicatively up to $1+\varepsilon$. We introduce a new complexity parameter, which depends on the geometry of $T$, and show that it suffices to choose $s$ and $m$ such that this parameter is small. Our result is a sparse analog of Gordon's theorem, which was concerned with a dense $\Phi$ having i.i.d. Gaussian entries. We qualitatively unify several results related to the Johnson-Lindenstrauss lemma, subspace embeddings, and Fourier-based restricted isometries. Our work also implies new results in using the sparse Johnson-Lindenstrauss transform in numerical linear algebra, classical and model-based compressed sensing, manifold learning, and constrained least squares problems such as the Lasso.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge