The Geometry of Deep Networks: Power Diagram Subdivision
Paper and Code
May 21, 2019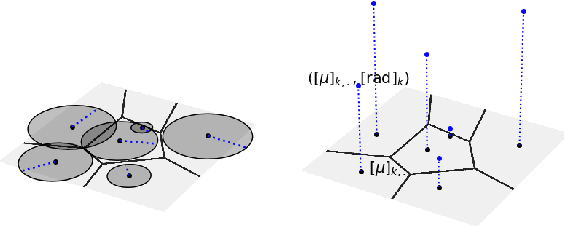
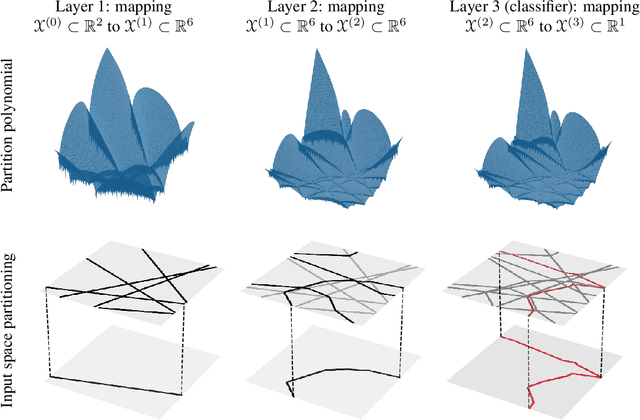

We study the geometry of deep (neural) networks (DNs) with piecewise affine and convex nonlinearities. The layers of such DNs have been shown to be {\em max-affine spline operators} (MASOs) that partition their input space and apply a region-dependent affine mapping to their input to produce their output. We demonstrate that each MASO layer's input space partitioning corresponds to a {\em power diagram} (an extension of the classical Voronoi tiling) with a number of regions that grows exponentially with respect to the number of units (neurons). We further show that a composition of MASO layers (e.g., the entire DN) produces a progressively subdivided power diagram and provide its analytical form. The subdivision process constrains the affine maps on the (exponentially many) power diagram regions to greatly reduce their complexity. For classification problems, we obtain a formula for a MASO DN's decision boundary in the input space plus a measure of its curvature that depends on the DN's nonlinearities, weights, and architecture. Numerous numerical experiments support and extend our theoretical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge