Statistical Inference for Optimal Transport Maps: Recent Advances and Perspectives
Paper and Code
Jun 23, 2025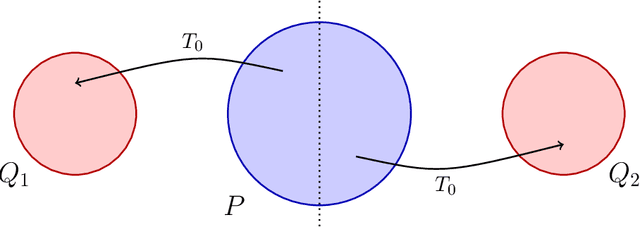
In many applications of optimal transport (OT), the object of primary interest is the optimal transport map. This map rearranges mass from one probability distribution to another in the most efficient way possible by minimizing a specified cost. In this paper we review recent advances in estimating and developing limit theorems for the OT map, using samples from the underlying distributions. We also review parallel lines of work that establish similar results for special cases and variants of the basic OT setup. We conclude with a discussion of key directions for future research with the goal of providing practitioners with reliable inferential tools.
* 36 pages, 1 figure
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge