Sharp Statistical Guarantees for Adversarially Robust Gaussian Classification
Paper and Code
Jun 29, 2020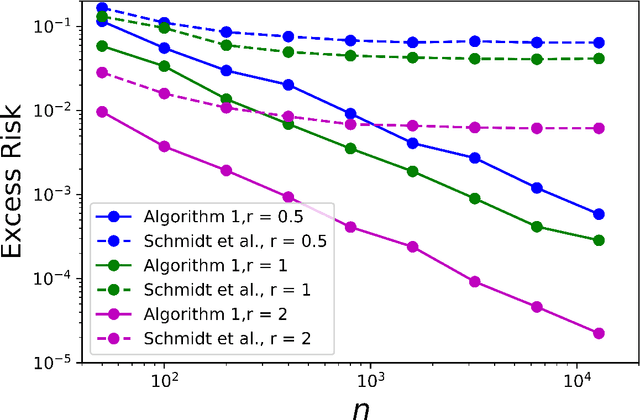
Adversarial robustness has become a fundamental requirement in modern machine learning applications. Yet, there has been surprisingly little statistical understanding so far. In this paper, we provide the first result of the optimal minimax guarantees for the excess risk for adversarially robust classification, under Gaussian mixture model proposed by \cite{schmidt2018adversarially}. The results are stated in terms of the Adversarial Signal-to-Noise Ratio (AdvSNR), which generalizes a similar notion for standard linear classification to the adversarial setting. For the Gaussian mixtures with AdvSNR value of $r$, we establish an excess risk lower bound of order $\Theta(e^{-(\frac{1}{8}+o(1)) r^2} \frac{d}{n})$ and design a computationally efficient estimator that achieves this optimal rate. Our results built upon minimal set of assumptions while cover a wide spectrum of adversarial perturbations including $\ell_p$ balls for any $p \ge 1$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge