Semi-Orthogonal Non-Negative Matrix Factorization

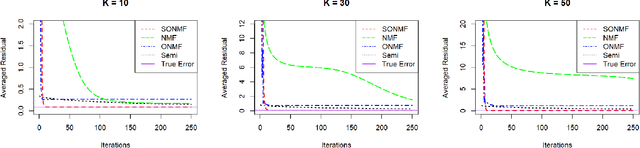
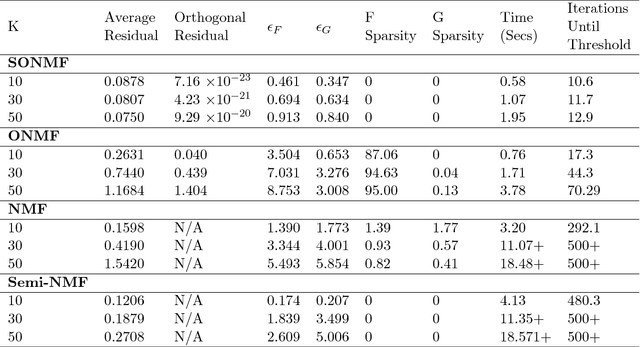
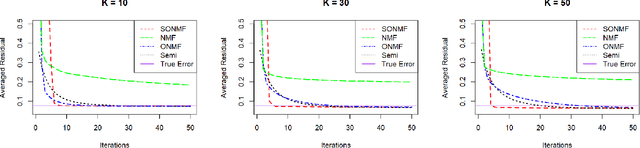
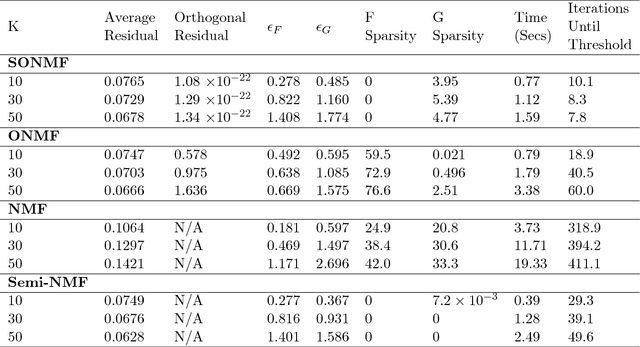
Non-negative Matrix Factorization (NMF) is a popular clustering and dimension reduction method by decomposing a non-negative matrix into the product of two lower dimension matrices composed of basis vectors. In this paper, we propose semi-orthogonal NMF, a novel method that enforces one of the matrices to be orthogonal with mixed signs. Our method preserves strict orthogonality by implementing the Cayley transformation to force the solution path to be exactly on the Stiefel manifold, as opposed to the approximated orthogonality solutions in existing literature. We apply a line search update scheme along with an SVD-based initialization which produces a rapid convergence of the algorithm compared to other existing approaches. In addition, we present formulations of our method to incorporate both continuous and binary design matrices. Through various simulation studies, we show that our model has an advantage over other NMF variations regarding the accuracy of the factorization, rate of convergence, and the degree of orthogonality while being computationally competitive. We also apply our method to a text mining application on classifying triage notes and show the effectiveness of our model in increasing classification accuracy compared to the conventional bag-of-words model and other alternative matrix factorization approaches. The proposed methods, along with a variety of existing non-negative matrix factorization approaches, are implemented in the R package `MatrixFact', which is available on GitHub.