Registering Image Volumes using 3D SIFT and Discrete SP-Symmetry
Paper and Code
May 30, 2022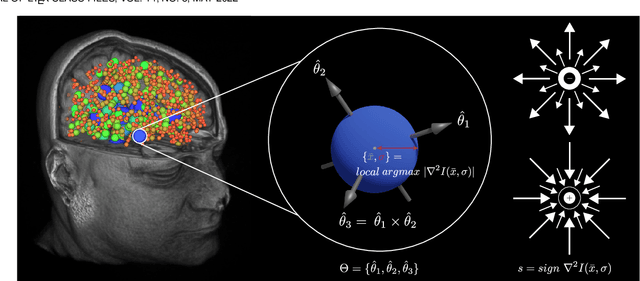
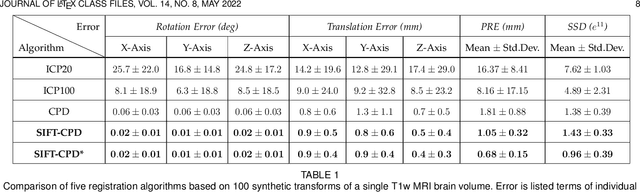
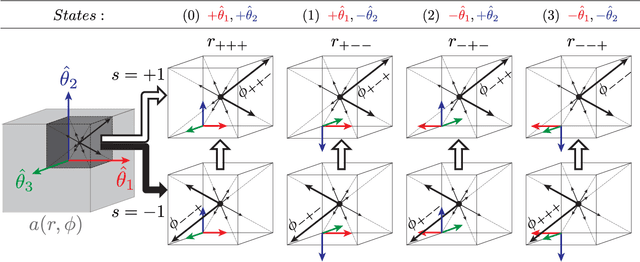
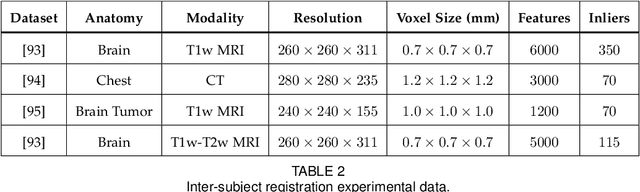
This paper proposes to extend local image features in 3D to include invariance to discrete symmetry including inversion of spatial axes and image contrast. A binary feature sign $s \in \{-1,+1\}$ is defined as the sign of the Laplacian operator $\nabla^2$, and used to obtain a descriptor that is invariant to image sign inversion $s \rightarrow -s$ and 3D parity transforms $(x,y,z)\rightarrow(-x,-y,-z)$, i.e. SP-invariant or SP-symmetric. SP-symmetry applies to arbitrary scalar image fields $I: R^3 \rightarrow R^1$ mapping 3D coordinates $(x,y,z) \in R^3$ to scalar intensity $I(x,y,z) \in R^1$, generalizing the well-known charge conjugation and parity symmetry (CP-symmetry) applying to elementary charged particles. Feature orientation is modeled as a set of discrete states corresponding to potential axis reflections, independently of image contrast inversion. Two primary axis vectors are derived from image observations and potentially subject to reflection, and a third axis is an axial vector defined by the right-hand rule. Augmenting local feature properties with sign in addition to standard (location, scale, orientation) geometry leads to descriptors that are invariant to coordinate reflections and intensity contrast inversion. Feature properties are factored in to probabilistic point-based registration as symmetric kernels, based on a model of binary feature correspondence. Experiments using the well-known coherent point drift (CPD) algorithm demonstrate that SIFT-CPD kernels achieve the most accurate and rapid registration of the human brain and CT chest, including multiple MRI modalities of differing intensity contrast, and abnormal local variations such as tumors or occlusions. SIFT-CPD image registration is invariant to global scaling, rotation and translation and image intensity inversions of the input data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge