Rapid Posterior Exploration in Bayesian Non-negative Matrix Factorization
Paper and Code
Oct 27, 2016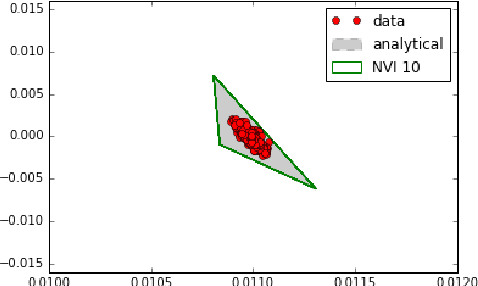

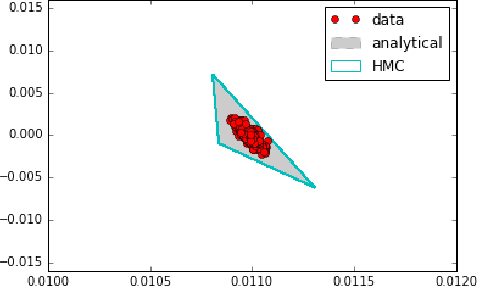
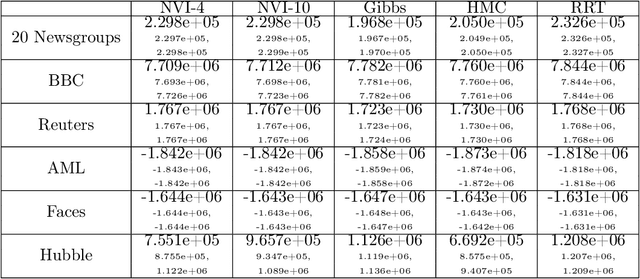
Non-negative Matrix Factorization (NMF) is a popular tool for data exploration. Bayesian NMF promises to also characterize uncertainty in the factorization. Unfortunately, current inference approaches such as MCMC mix slowly and tend to get stuck on single modes. We introduce a novel approach using rapidly-exploring random trees (RRTs) to asymptotically cover regions of high posterior density. These are placed in a principled Bayesian framework via an online extension to nonparametric variational inference. On experiments on real and synthetic data, we obtain greater coverage of the posterior and higher ELBO values than standard NMF inference approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge