PopSGD: Decentralized Stochastic Gradient Descent in the Population Model

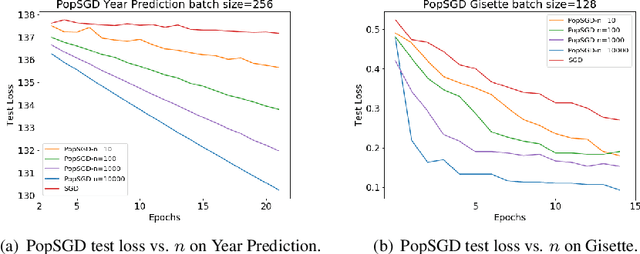
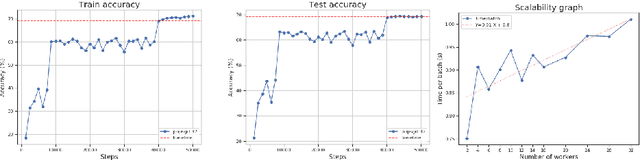
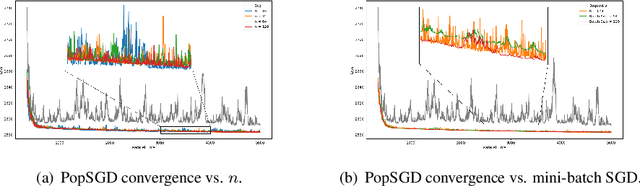
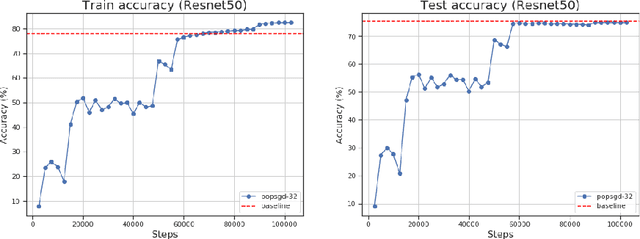
The population model is a standard way to represent large-scale decentralized distributed systems, in which agents with limited computational power interact in randomly chosen pairs, in order to collectively solve global computational tasks. In contrast with synchronous gossip models, nodes are anonymous, lack a common notion of time, and have no control over their scheduling. In this paper, we examine whether large-scale distributed optimization can be performed in this extremely restrictive setting. We introduce and analyze a natural decentralized variant of stochastic gradient descent (SGD), called PopSGD, in which every node maintains a local parameter, and is able to compute stochastic gradients with respect to this parameter. Every pair-wise node interaction performs a stochastic gradient step at each agent, followed by averaging of the two models. We prove that, under standard assumptions, SGD can converge even in this extremely loose, decentralized setting, for both convex and non-convex objectives. Moreover, surprisingly, in the former case, the algorithm can achieve linear speedup in the number of nodes $n$. Our analysis leverages a new technical connection between decentralized SGD and randomized load-balancing, which enables us to tightly bound the concentration of node parameters. We validate our analysis through experiments, showing that PopSGD can achieve convergence and speedup for large-scale distributed learning tasks in a supercomputing environment.