Optimal classification in sparse Gaussian graphic model
Paper and Code
Nov 20, 2013
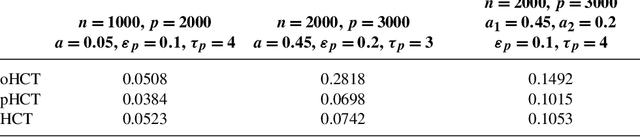

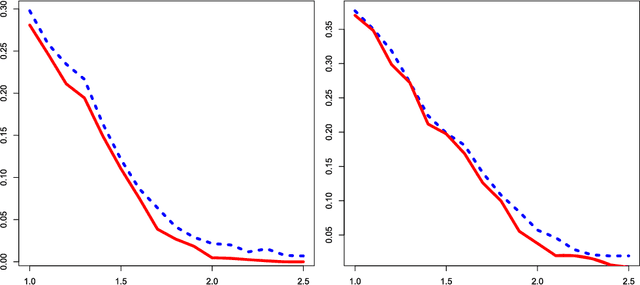
Consider a two-class classification problem where the number of features is much larger than the sample size. The features are masked by Gaussian noise with mean zero and covariance matrix $\Sigma$, where the precision matrix $\Omega=\Sigma^{-1}$ is unknown but is presumably sparse. The useful features, also unknown, are sparse and each contributes weakly (i.e., rare and weak) to the classification decision. By obtaining a reasonably good estimate of $\Omega$, we formulate the setting as a linear regression model. We propose a two-stage classification method where we first select features by the method of Innovated Thresholding (IT), and then use the retained features and Fisher's LDA for classification. In this approach, a crucial problem is how to set the threshold of IT. We approach this problem by adapting the recent innovation of Higher Criticism Thresholding (HCT). We find that when useful features are rare and weak, the limiting behavior of HCT is essentially just as good as the limiting behavior of ideal threshold, the threshold one would choose if the underlying distribution of the signals is known (if only). Somewhat surprisingly, when $\Omega$ is sufficiently sparse, its off-diagonal coordinates usually do not have a major influence over the classification decision. Compared to recent work in the case where $\Omega$ is the identity matrix [Proc. Natl. Acad. Sci. USA 105 (2008) 14790-14795; Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 367 (2009) 4449-4470], the current setting is much more general, which needs a new approach and much more sophisticated analysis. One key component of the analysis is the intimate relationship between HCT and Fisher's separation. Another key component is the tight large-deviation bounds for empirical processes for data with unconventional correlation structures, where graph theory on vertex coloring plays an important role.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge