Neumann Networks for Inverse Problems in Imaging
Paper and Code
Jan 13, 2019
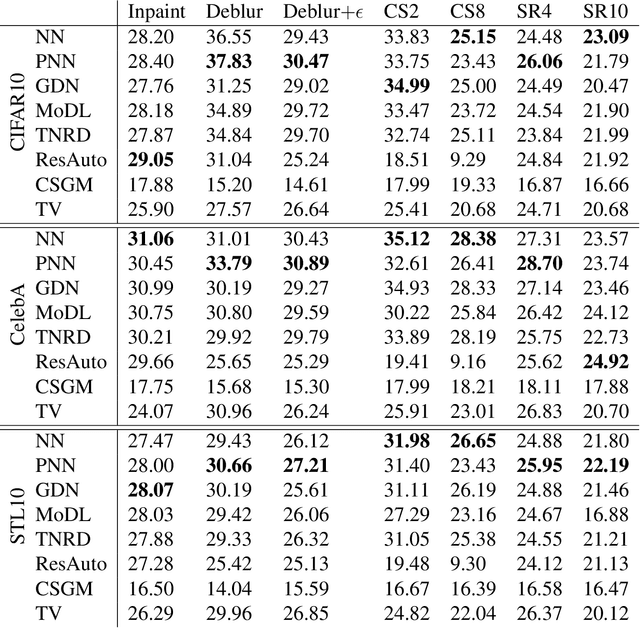
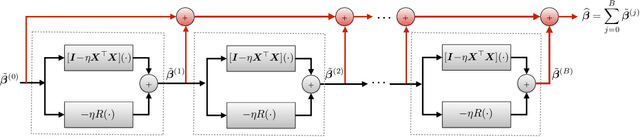

Many challenging image processing tasks can be described by an ill-posed linear inverse problem: deblurring, deconvolution, inpainting, compressed sensing, and superresolution all lie in this framework. Traditional inverse problem solvers minimize a cost function consisting of a data-fit term, which measures how well an image matches the observations, and a regularizer, which reflects prior knowledge and promotes images with desirable properties like smoothness. Recent advances in machine learning and image processing have illustrated that it is often possible to learn a regularizer from training data that can outperform more traditional regularizers. We present an end-to-end, data-driven method of solving inverse problems inspired by the Neumann series, which we call a Neumann network. Rather than unroll an iterative optimization algorithm, we truncate a Neumann series which directly solves the linear inverse problem with a data-driven nonlinear regularizer. The Neumann network architecture outperforms traditional inverse problem solution methods, model-free deep learning approaches, and state-of-the-art unrolled iterative methods on standard datasets. Finally, when the images belong to a union of subspaces and under appropriate assumptions on the forward model, we prove there exists a Neumann network configuration that well-approximates the optimal oracle estimator for the inverse problem and demonstrate empirically that the trained Neumann network has the form predicted by theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge