High-dimensional Index Volatility Models via Stein's Identity

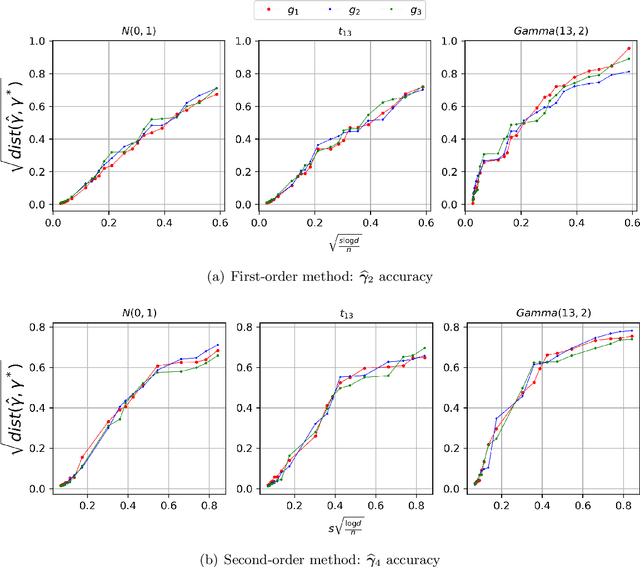
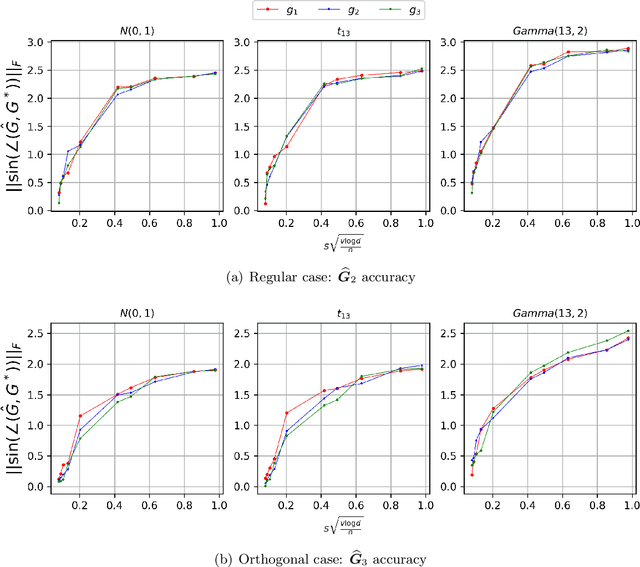
In this paper, we consider estimating the parametric components of index volatility models, whose variance function has semiparametric form with two common index structures: single index and multiple index. Our approach applies the first- and second-order Stein's identities on the empirical mean squared error (MSE) to extract the direction of true signals. We study both low-dimensional setting and high-dimensional setting under finite moment condition, which is weaker than existing literature and makes our estimators applicable even for some heavy-tailed data. From our theoretical analysis, we prove that the statistical rate of convergence has two components: parametric rate and nonparametric rate. For the parametric rate, we achieve $\sqrt{n}$-consistency for low-dimensional setting and optimal/sub-optimal rate for high-dimensional setting. For the nonparametric rate, we show it's asymptotically bounded by $n^{-4/5}$ under both settings when the mean function has bounded second derivative, so it only contributes high-order terms. Simulation results also back our theoretical conclusions.