Harmonizing Geometry and Uncertainty: Diffusion with Hyperspheres
Paper and Code
Jun 12, 2025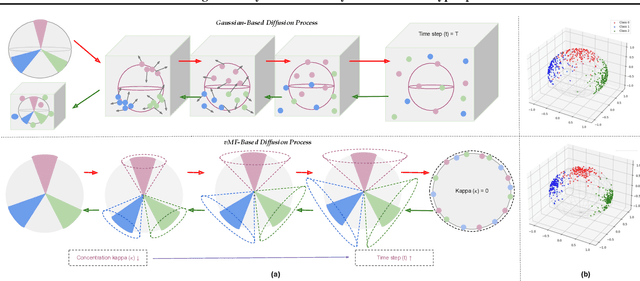
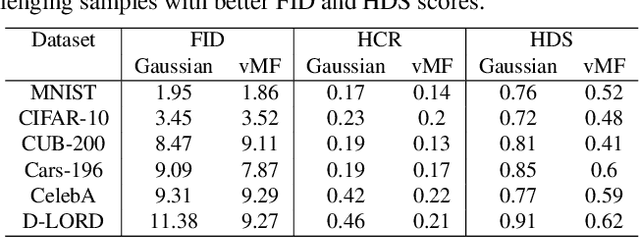


Do contemporary diffusion models preserve the class geometry of hyperspherical data? Standard diffusion models rely on isotropic Gaussian noise in the forward process, inherently favoring Euclidean spaces. However, many real-world problems involve non-Euclidean distributions, such as hyperspherical manifolds, where class-specific patterns are governed by angular geometry within hypercones. When modeled in Euclidean space, these angular subtleties are lost, leading to suboptimal generative performance. To address this limitation, we introduce HyperSphereDiff to align hyperspherical structures with directional noise, preserving class geometry and effectively capturing angular uncertainty. We demonstrate both theoretically and empirically that this approach aligns the generative process with the intrinsic geometry of hyperspherical data, resulting in more accurate and geometry-aware generative models. We evaluate our framework on four object datasets and two face datasets, showing that incorporating angular uncertainty better preserves the underlying hyperspherical manifold. Resources are available at: {https://github.com/IAB-IITJ/Harmonizing-Geometry-and-Uncertainty-Diffusion-with-Hyperspheres/}
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge