Empirical confidence estimates for classification by deep neural networks

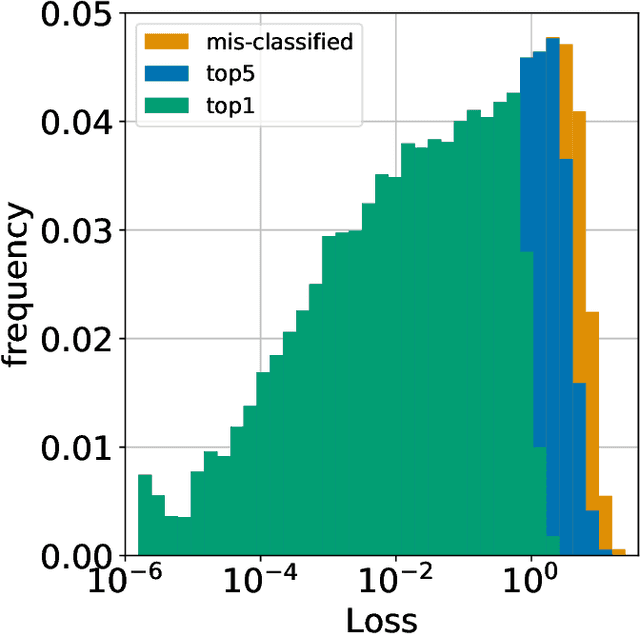
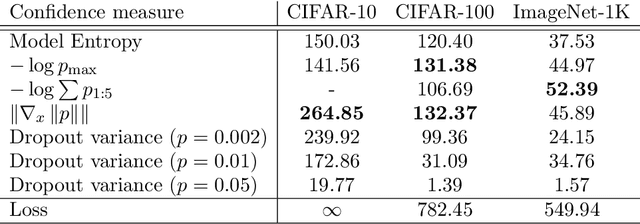
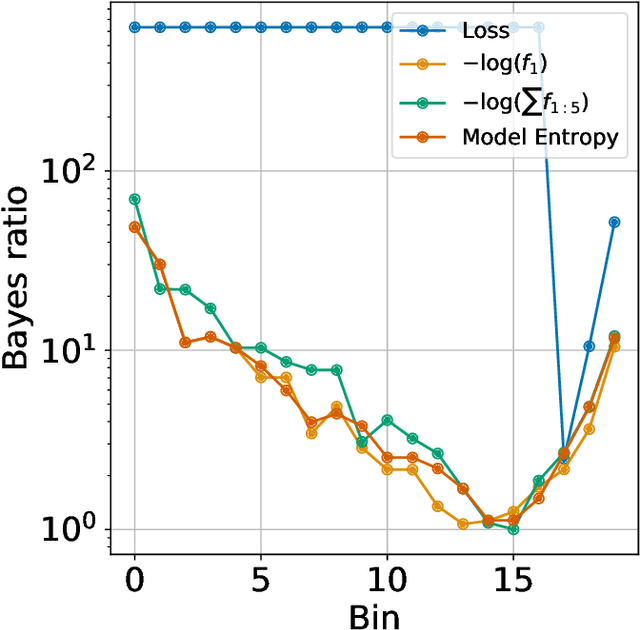
How well can we estimate the probability that the classification, $C(f(x))$, predicted by a deep neural network is correct (or in the Top 5)? We consider the case of a classification neural network trained with the KL divergence which is assumed to generalize, as measured empirically by the test error and test loss. We present conditional probabilities for predictions based on the histogram of uncertainty metrics, which have a significant Bayes ratio. Previous work in this area includes Bayesian neural networks. Our metric is twice as predictive, based on the expected Bayes ratio, on ImageNet compared to our best tuned implementation of Bayesian dropout~\cite{gal2016dropout}. Our method uses just the softmax values and a stored histogram so it is essentially free to compute, compared to many times inference cost for Bayesian dropout.