Efficient Conversion of Bayesian Network Learning into Quadratic Unconstrained Binary Optimization

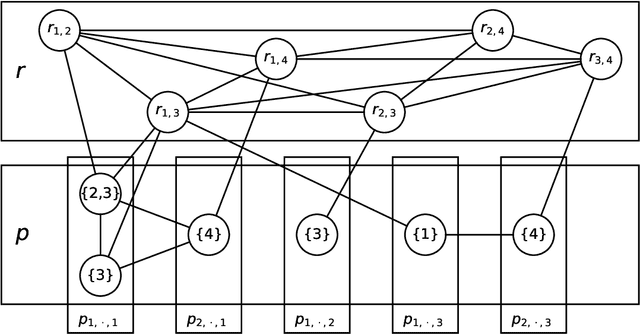
Ising machines (IMs) are a potential breakthrough in the NP-hard problem of score-based Bayesian network (BN) learning. To utilize the power of IMs, encoding of BN learning into quadratic unconstrained binary optimization (QUBO) has been proposed using up to $\mathcal{O}(N^2)$ bits, for $N$ variables in BN and $M = 2$ parents each. However, this approach is usually infeasible owing to the upper bound of IM bits when $M \geq 3$. In this paper, we propose an efficient conversion method for BN learning into QUBO with a maximum of $\sum_n (\Lambda_n - 1) + \binom N2$ bits, for $\Lambda_n$ parent set candidates each. The advance selection of parent set candidates plays an essential role in reducing the number of required bits. We also develop a pre-processing algorithm based on the capabilities of a classification and regression tree (CART), which allows us to search for parent set candidates consistent with score minimization in a realistic timeframe.Our conversion method enables us to more significantly reduce the upper bound of the required bits in comparison to an existing method, and is therefore expected to make a significant contribution to the advancement of scalable score-based BN learning.