Differentiable Particle Filtering without Modifying the Forward Pass

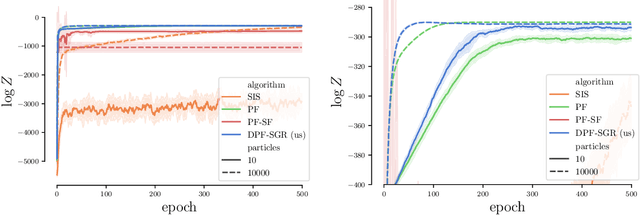
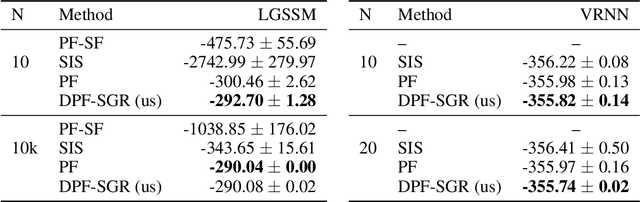
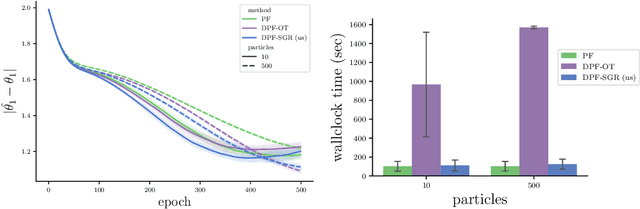
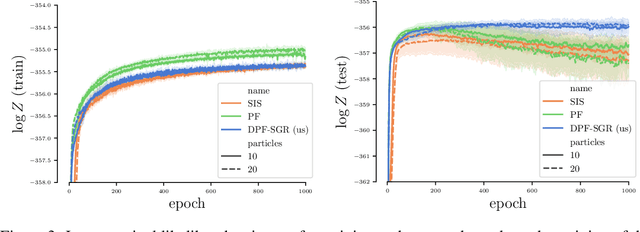
In recent years particle filters have being used as components in systems optimized end-to-end with gradient descent. However, the resampling step in a particle filter is not differentiable, which biases gradients and interferes with optimization. To remedy this problem, several differentiable variants of resampling have been proposed, all of which modify the behavior of the particle filter in significant and potentially undesirable ways. In this paper, we show how to obtain unbiased estimators of the gradient of the marginal likelihood by only modifying messages used in backpropagation, leaving the standard forward pass of a particle filter unchanged. Our method is simple to implement, has a low computational overhead, does not introduce additional hyperparameters, and extends to derivatives of higher orders. We call it stop-gradient resampling, since it can easily be implemented with automatic differentiation libraries using the stop-gradient operator instead of explicitly modifying the backward messages.