Community Detection in Sparse Random Networks

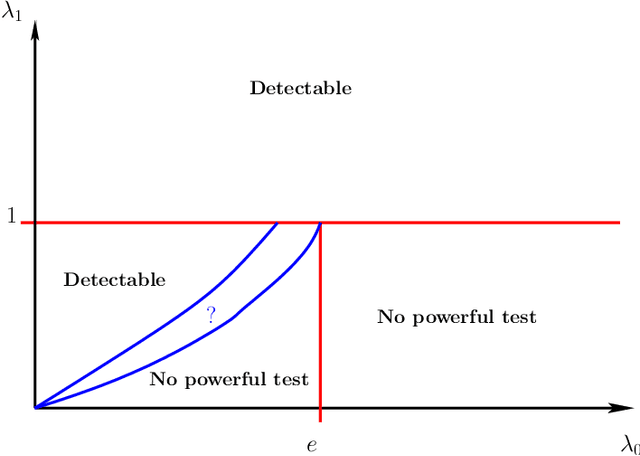
We consider the problem of detecting a tight community in a sparse random network. This is formalized as testing for the existence of a dense random subgraph in a random graph. Under the null hypothesis, the graph is a realization of an Erd\"os-R\'enyi graph on $N$ vertices and with connection probability $p_0$; under the alternative, there is an unknown subgraph on $n$ vertices where the connection probability is p1 > p0. In Arias-Castro and Verzelen (2012), we focused on the asymptotically dense regime where p0 is large enough that np0>(n/N)^{o(1)}. We consider here the asymptotically sparse regime where p0 is small enough that np0<(n/N)^{c0} for some c0>0. As before, we derive information theoretic lower bounds, and also establish the performance of various tests. Compared to our previous work, the arguments for the lower bounds are based on the same technology, but are substantially more technical in the details; also, the methods we study are different: besides a variant of the scan statistic, we study other statistics such as the size of the largest connected component, the number of triangles, the eigengap of the adjacency matrix, etc. Our detection bounds are sharp, except in the Poisson regime where we were not able to fully characterize the constant arising in the bound.