An Evaluation of Structural Parameters for Probabilistic Reasoning: Results on Benchmark Circuits
Paper and Code
Feb 13, 2013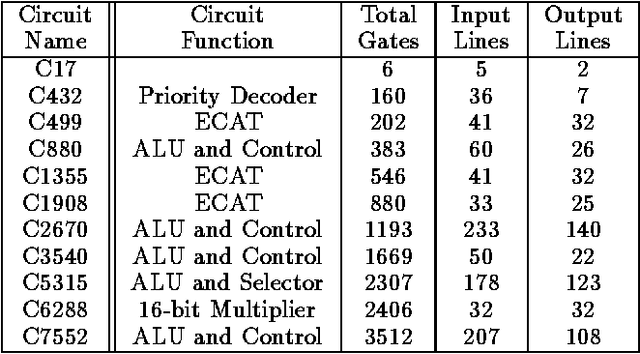
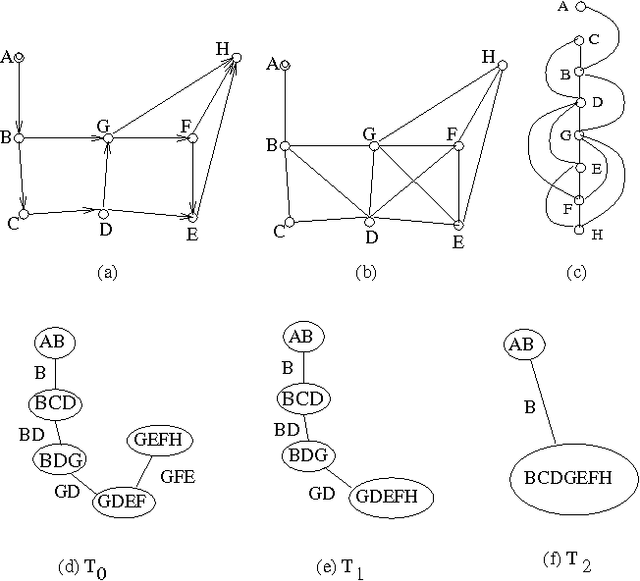
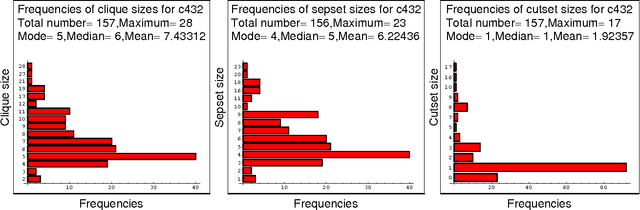

Many algorithms for processing probabilistic networks are dependent on the topological properties of the problem's structure. Such algorithms (e.g., clustering, conditioning) are effective only if the problem has a sparse graph captured by parameters such as tree width and cycle-cut set size. In this paper we initiate a study to determine the potential of structure-based algorithms in real-life applications. We analyze empirically the structural properties of problems coming from the circuit diagnosis domain. Specifically, we locate those properties that capture the effectiveness of clustering and conditioning as well as of a family of conditioning+clustering algorithms designed to gradually trade space for time. We perform our analysis on 11 benchmark circuits widely used in the testing community. We also report on the effect of ordering heuristics on tree-clustering and show that, on our benchmarks, the well-known max-cardinality ordering is substantially inferior to an ordering called min-degree.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge