An efficient projection neural network for $\ell_1$-regularized logistic regression

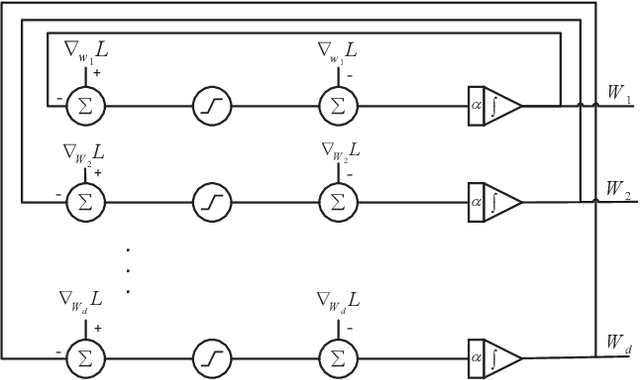
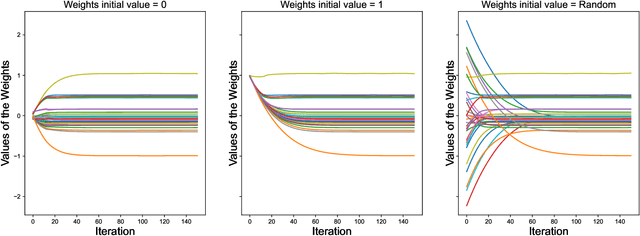
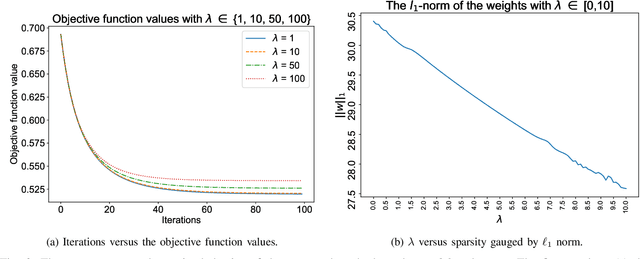
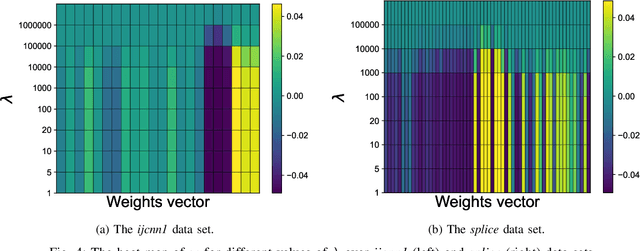
$\ell_1$ regularization has been used for logistic regression to circumvent the overfitting and use the estimated sparse coefficient for feature selection. However, the challenge of such a regularization is that the $\ell_1$ norm is not differentiable, making the standard algorithms for convex optimization not applicable to this problem. This paper presents a simple projection neural network for $\ell_1$-regularized logistics regression. In contrast to many available solvers in the literature, the proposed neural network does not require any extra auxiliary variable nor any smooth approximation, and its complexity is almost identical to that of the gradient descent for logistic regression without $\ell_1$ regularization, thanks to the projection operator. We also investigate the convergence of the proposed neural network by using the Lyapunov theory and show that it converges to a solution of the problem with any arbitrary initial value. The proposed neural solution significantly outperforms state-of-the-art methods with respect to the execution time and is competitive in terms of accuracy and AUROC.