Algorithms for Efficiently Learning Low-Rank Neural Networks

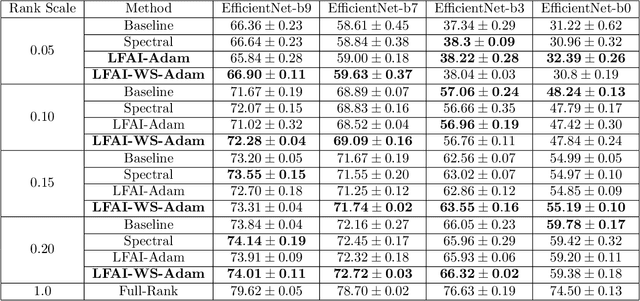
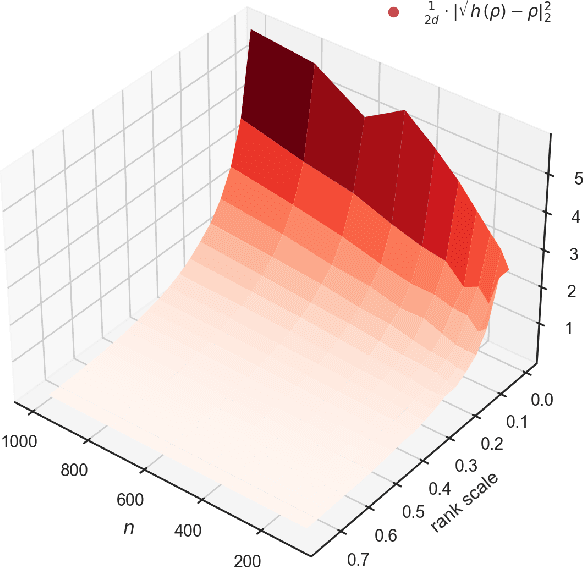
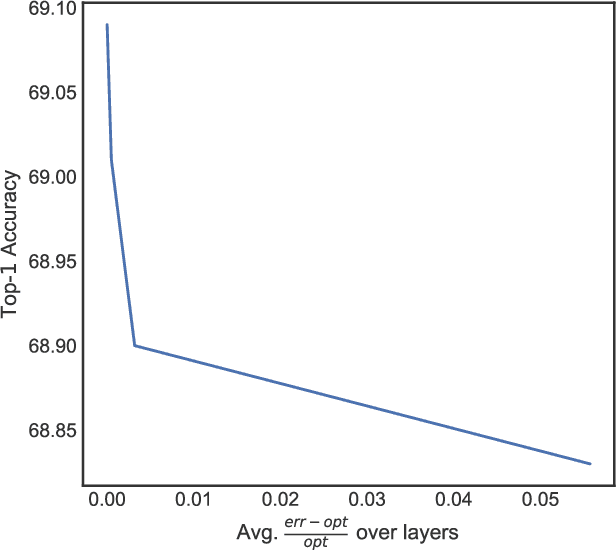
We study algorithms for learning low-rank neural networks -- networks where the weight parameters are re-parameterized by products of two low-rank matrices. First, we present a provably efficient algorithm which learns an optimal low-rank approximation to a single-hidden-layer ReLU network up to additive error $\epsilon$ with probability $\ge 1 - \delta$, given access to noiseless samples with Gaussian marginals in polynomial time and samples. Thus, we provide the first example of an algorithm which can efficiently learn a neural network up to additive error without assuming the ground truth is realizable. To solve this problem, we introduce an efficient SVD-based $\textit{Nonlinear Kernel Projection}$ algorithm for solving a nonlinear low-rank approximation problem over Gaussian space. Inspired by the efficiency of our algorithm, we propose a novel low-rank initialization framework for training low-rank $\textit{deep}$ networks, and prove that for ReLU networks, the gap between our method and existing schemes widens as the desired rank of the approximating weights decreases, or as the dimension of the inputs increases (the latter point holds when network width is superlinear in dimension). Finally, we validate our theory by training ResNet and EfficientNet models on ImageNet.