A Tight Bound for Stochastic Submodular Cover
Paper and Code
Feb 01, 2021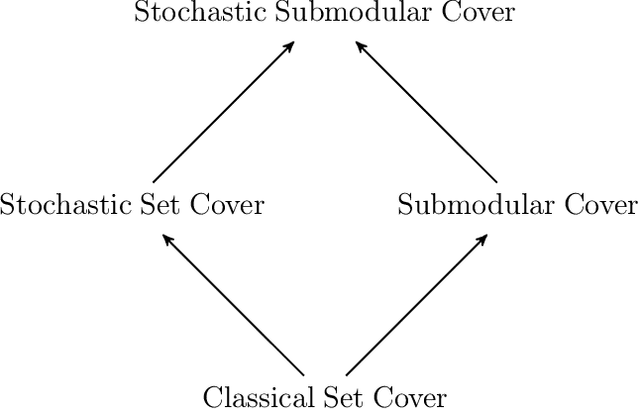

We show that the Adaptive Greedy algorithm of Golovin and Krause (2011) achieves an approximation bound of $(\ln (Q/\eta)+1)$ for Stochastic Submodular Cover: here $Q$ is the "goal value" and $\eta$ is the smallest non-zero marginal increase in utility deliverable by an item. (For integer-valued utility functions, we show a bound of $H(Q)$, where $H(Q)$ is the $Q^{th}$ Harmonic number.) Although this bound was claimed by Golovin and Krause in the original version of their paper, the proof was later shown to be incorrect by Nan and Saligrama (2017). The subsequent corrected proof of Golovin and Krause (2017) gives a quadratic bound of $(\ln(Q/\eta) + 1)^2$. Other previous bounds for the problem are $56(\ln(Q/\eta) + 1)$, implied by work of Im et al. (2016) on a related problem, and $k(\ln (Q/\eta)+1)$, due to Deshpande et al. (2016) and Hellerstein and Kletenik (2018), where $k$ is the number of states. Our bound generalizes the well-known $(\ln~m + 1)$ approximation bound on the greedy algorithm for the classical Set Cover problem, where $m$ is the size of the ground set.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge