A New Index for Clustering Evaluation Based on Density Estimation
Paper and Code
Jul 11, 2022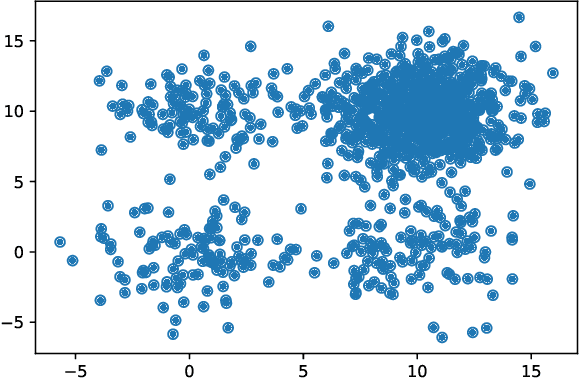

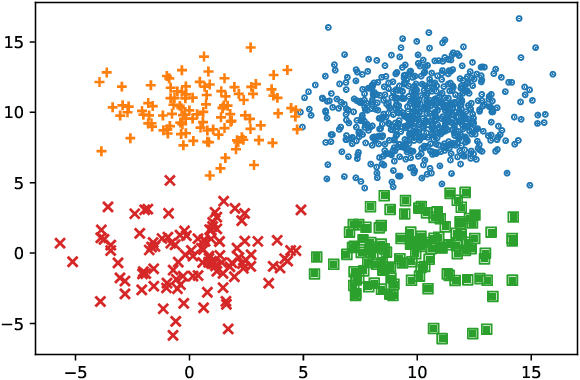
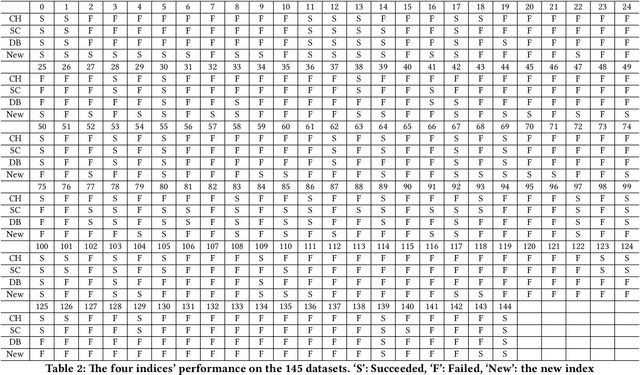
A new index for internal evaluation of clustering is introduced. The index is defined as a mixture of two sub-indices. The first sub-index $ I_a $ is called the Ambiguous Index; the second sub-index $ I_s $ is called the Similarity Index. Calculation of the two sub-indices is based on density estimation to each cluster of a partition of the data. An experiment is conducted to test the performance of the new index, and compared with three popular internal clustering evaluation indices -- Calinski-Harabasz index, Silhouette coefficient, and Davies-Bouldin index, on a set of 145 datasets. The result shows the new index improves the three popular indices by 59%, 34%, and 74%, correspondingly.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge