A flexible PageRank-based graph embedding framework closely related to spectral eigenvector embeddings
Paper and Code
Jul 22, 2022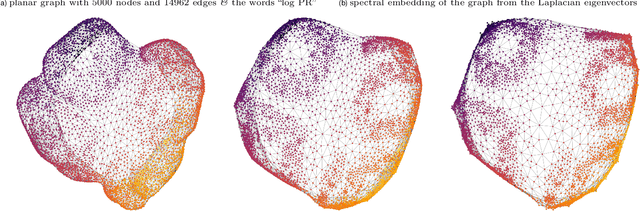
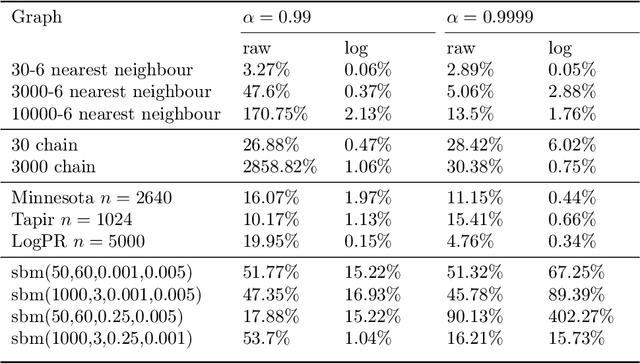
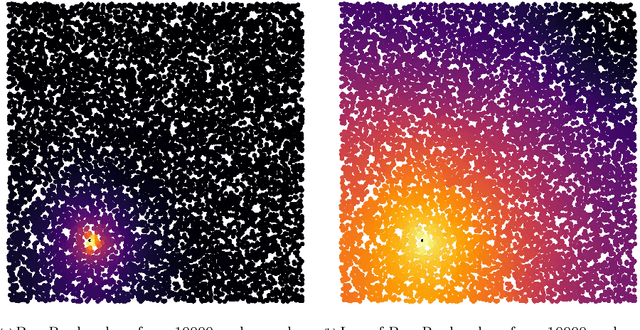
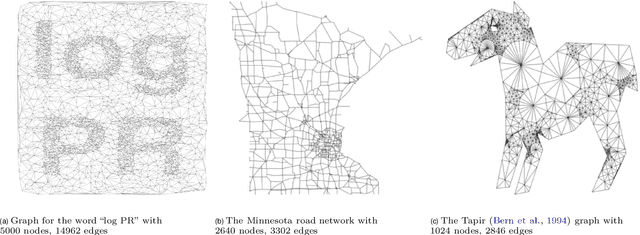
We study a simple embedding technique based on a matrix of personalized PageRank vectors seeded on a random set of nodes. We show that the embedding produced by the element-wise logarithm of this matrix (1) are related to the spectral embedding for a class of graphs where spectral embeddings are significant, and hence useful representation of the data, (2) can be done for the entire network or a smaller part of it, which enables precise local representation, and (3) uses a relatively small number of PageRank vectors compared to the size of the networks. Most importantly, the general nature of this embedding strategy opens up many emerging applications, where eigenvector and spectral techniques may not be well established, to the PageRank-based relatives. For instance, similar techniques can be used on PageRank vectors from hypergraphs to get "spectral-like" embeddings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge