AGENet: Adaptive Edge-aware Geodesic Distance Learning for Few-Shot Medical Image Segmentation

Medical image segmentation requires large annotated datasets, creating a significant bottleneck for clinical applications. While few-shot segmentation methods can learn from minimal examples, existing approaches demonstrate suboptimal performance in precise boundary delineation for medical images, particularly when anatomically similar regions appear without sufficient spatial context. We propose AGENet (Adaptive Geodesic Edge-aware Network), a novel framework that incorporates spatial relationships through edge-aware geodesic distance learning. Our key insight is that medical structures follow predictable geometric patterns that can guide prototype extraction even with limited training data. Unlike methods relying on complex architectural components or heavy neural networks, our approach leverages computationally lightweight geometric modeling. The framework combines three main components: (1) An edge-aware geodesic distance learning module that respects anatomical boundaries through iterative Fast Marching refinement, (2) adaptive prototype extraction that captures both global structure and local boundary details via spatially-weighted aggregation, and (3) adaptive parameter learning that automatically adjusts to different organ characteristics. Extensive experiments across diverse medical imaging datasets demonstrate improvements over state-of-the-art methods. Notably, our method reduces boundary errors compared to existing approaches while maintaining computational efficiency, making it highly suitable for clinical applications requiring precise segmentation with limited annotated data.

SWE-Compass: Towards Unified Evaluation of Agentic Coding Abilities for Large Language Models

Evaluating large language models (LLMs) for software engineering has been limited by narrow task coverage, language bias, and insufficient alignment with real-world developer workflows. Existing benchmarks often focus on algorithmic problems or Python-centric bug fixing, leaving critical dimensions of software engineering underexplored. To address these gaps, we introduce SWE-Compass1, a comprehensive benchmark that unifies heterogeneous code-related evaluations into a structured and production-aligned framework. SWE-Compass spans 8 task types, 8 programming scenarios, and 10 programming languages, with 2000 high-quality instances curated from authentic GitHub pull requests and refined through systematic filtering and validation. We benchmark ten state-of-the-art LLMs under two agentic frameworks, SWE-Agent and Claude Code, revealing a clear hierarchy of difficulty across task types, languages, and scenarios. Moreover, by aligning evaluation with real-world developer practices, SWE-Compass provides a rigorous and reproducible foundation for diagnosing and advancing agentic coding capabilities in large language models.

MDAS-GNN: Multi-Dimensional Spatiotemporal GNN with Spatial Diffusion for Urban Traffic Risk Forecasting

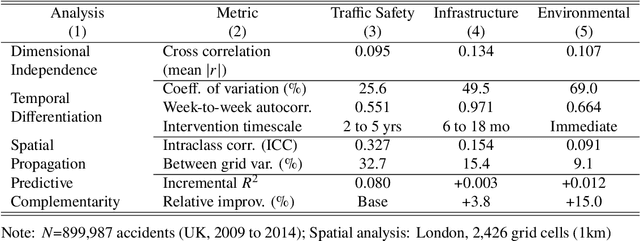
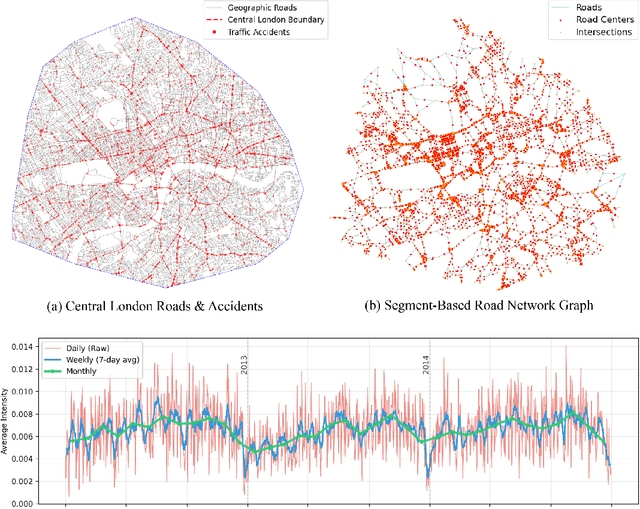
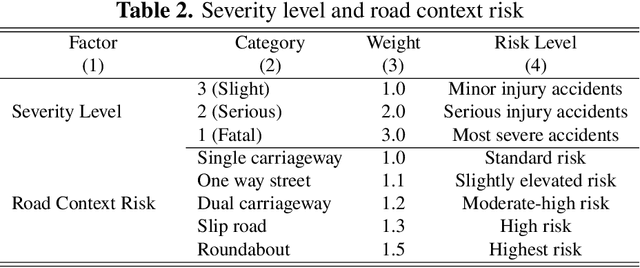
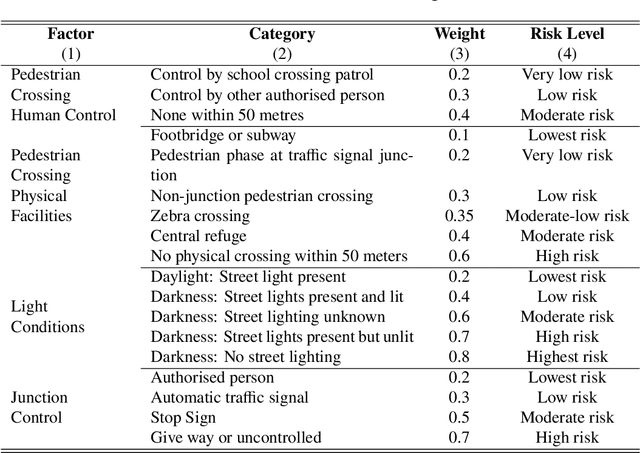
Traffic accidents represent a critical public health challenge, claiming over 1.35 million lives annually worldwide. Traditional accident prediction models treat road segments independently, failing to capture complex spatial relationships and temporal dependencies in urban transportation networks. This study develops MDAS-GNN, a Multi-Dimensional Attention-based Spatial-diffusion Graph Neural Network integrating three core risk dimensions: traffic safety, infrastructure, and environmental risk. The framework employs feature-specific spatial diffusion mechanisms and multi-head temporal attention to capture dependencies across different time horizons. Evaluated on UK Department for Transport accident data across Central London, South Manchester, and SE Birmingham, MDASGNN achieves superior performance compared to established baseline methods. The model maintains consistently low prediction errors across short, medium, and long-term periods, with particular strength in long-term forecasting. Ablation studies confirm that integrated multi-dimensional features outperform singlefeature approaches, reducing prediction errors by up to 40%. This framework provides civil engineers and urban planners with advanced predictive capabilities for transportation infrastructure design, enabling data-driven decisions for road network optimization, infrastructure resource improvements, and strategic safety interventions in urban development projects.

Preference-based Teaching

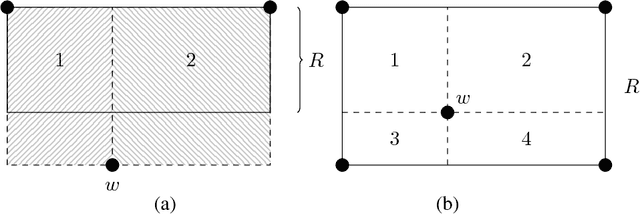
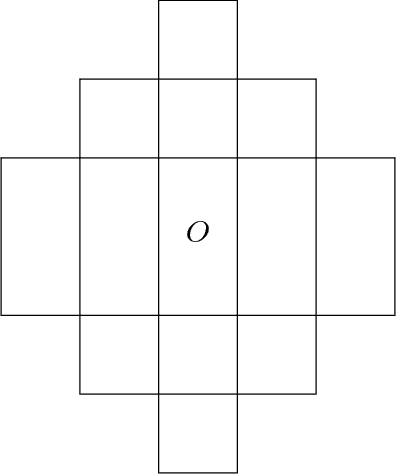
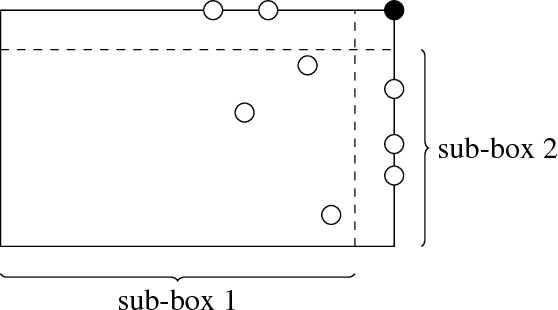
We introduce a new model of teaching named "preference-based teaching" and a corresponding complexity parameter---the preference-based teaching dimension (PBTD)---representing the worst-case number of examples needed to teach any concept in a given concept class. Although the PBTD coincides with the well-known recursive teaching dimension (RTD) on finite classes, it is radically different on infinite ones: the RTD becomes infinite already for trivial infinite classes (such as half-intervals) whereas the PBTD evaluates to reasonably small values for a wide collection of infinite classes including classes consisting of so-called closed sets w.r.t. a given closure operator, including various classes related to linear sets over $\mathbb{N}_0$ (whose RTD had been studied quite recently) and including the class of Euclidean half-spaces. On top of presenting these concrete results, we provide the reader with a theoretical framework (of a combinatorial flavor) which helps to derive bounds on the PBTD.

Combining Models of Approximation with Partial Learning

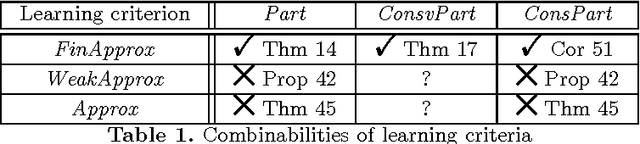
In Gold's framework of inductive inference, the model of partial learning requires the learner to output exactly one correct index for the target object and only the target object infinitely often. Since infinitely many of the learner's hypotheses may be incorrect, it is not obvious whether a partial learner can be modifed to "approximate" the target object. Fulk and Jain (Approximate inference and scientific method. Information and Computation 114(2):179--191, 1994) introduced a model of approximate learning of recursive functions. The present work extends their research and solves an open problem of Fulk and Jain by showing that there is a learner which approximates and partially identifies every recursive function by outputting a sequence of hypotheses which, in addition, are also almost all finite variants of the target function. The subsequent study is dedicated to the question how these findings generalise to the learning of r.e. languages from positive data. Here three variants of approximate learning will be introduced and investigated with respect to the question whether they can be combined with partial learning. Following the line of Fulk and Jain's research, further investigations provide conditions under which partial language learners can eventually output only finite variants of the target language. The combinabilities of other partial learning criteria will also be briefly studied.