Conditional Gradient Methods for convex optimization with function constraints

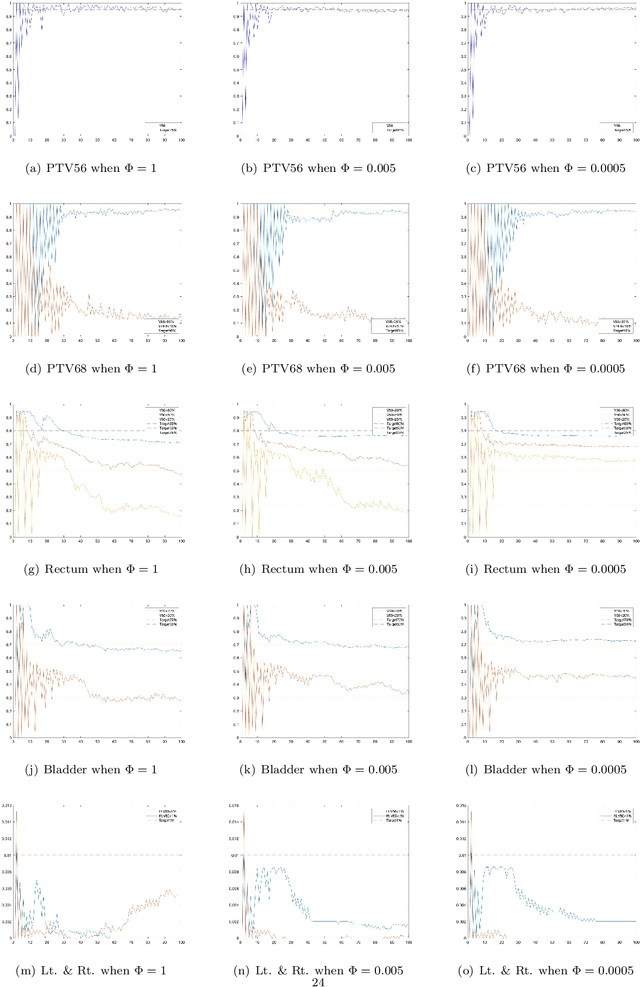
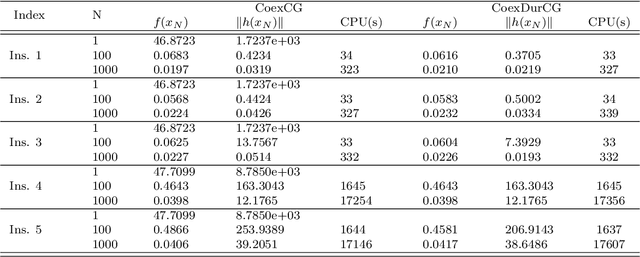
Conditional gradient methods have attracted much attention in both machine learning and optimization communities recently. These simple methods can guarantee the generation of sparse solutions. In addition, without the computation of full gradients, they can handle huge-scale problems sometimes even with an exponentially increasing number of decision variables. This paper aims to significantly expand the application areas of these methods by presenting new conditional gradient methods for solving convex optimization problems with general affine and nonlinear constraints. More specifically, we first present a new constraint extrapolated condition gradient (CoexCG) method that can achieve an ${\cal O}(1/\epsilon^2)$ iteration complexity for both smooth and structured nonsmooth function constrained convex optimization. We further develop novel variants of CoexCG, namely constraint extrapolated and dual regularized conditional gradient (CoexDurCG) methods, that can achieve similar iteration complexity to CoexCG but allow adaptive selection for algorithmic parameters. We illustrate the effectiveness of these methods for solving an important class of radiation therapy treatment planning problems arising from healthcare industry.

A Novel CNN-based Method for Accurate Ship Detection in HR Optical Remote Sensing Images via Rotated Bounding Box

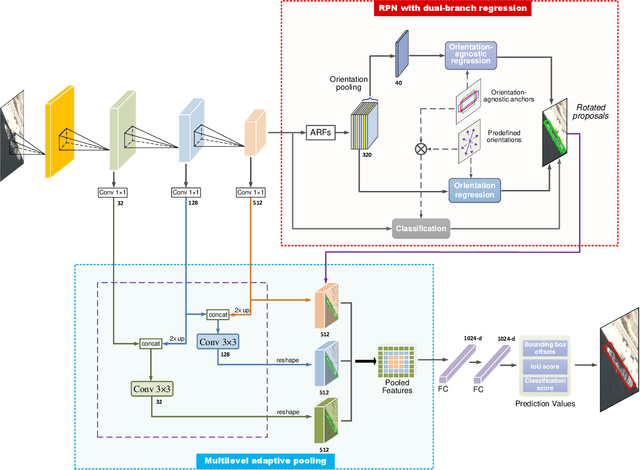
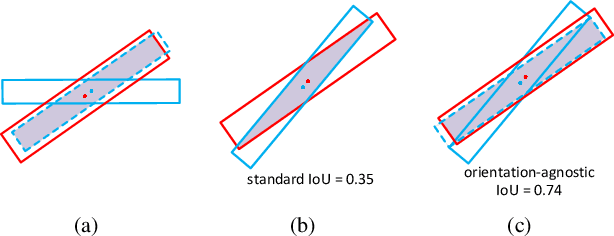
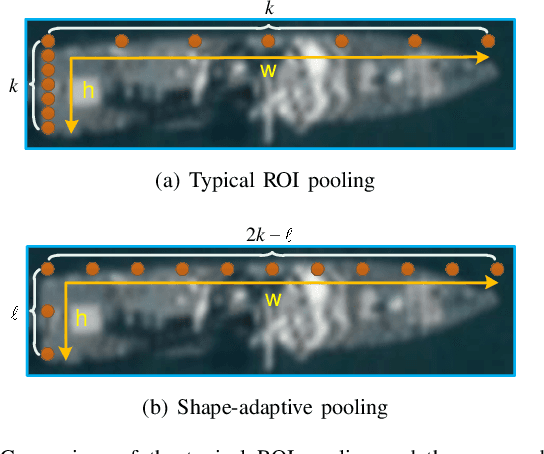
Currently, reliable and accurate ship detection in optical remote sensing images is still challenging. Even the state-of-the-art convolutional neural network (CNN) based methods cannot obtain very satisfactory results. To more accurately locate the ships in diverse orientations, some recent methods conduct the detection via the rotated bounding box. However, it further increases the difficulty of detection, because an additional variable of ship orientation must be accurately predicted in the algorithm. In this paper, a novel CNN-based ship detection method is proposed, by overcoming some common deficiencies of current CNN-based methods in ship detection. Specifically, to generate rotated region proposals, current methods have to predefine multi-oriented anchors, and predict all unknown variables together in one regression process, limiting the quality of overall prediction. By contrast, we are able to predict the orientation and other variables independently, and yet more effectively, with a novel dual-branch regression network, based on the observation that the ship targets are nearly rotation-invariant in remote sensing images. Next, a shape-adaptive pooling method is proposed, to overcome the limitation of typical regular ROI-pooling in extracting the features of the ships with various aspect ratios. Furthermore, we propose to incorporate multilevel features via the spatially-variant adaptive pooling. This novel approach, called multilevel adaptive pooling, leads to a compact feature representation more qualified for the simultaneous ship classification and localization. Finally, detailed ablation study performed on the proposed approaches is provided, along with some useful insights. Experimental results demonstrate the great superiority of the proposed method in ship detection.

Algorithms for stochastic optimization with expectation constraints

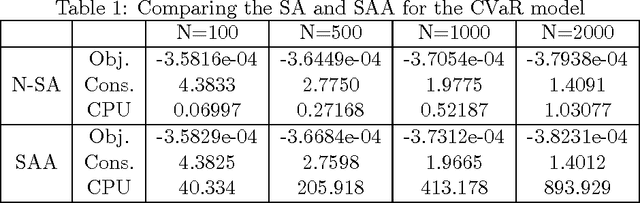
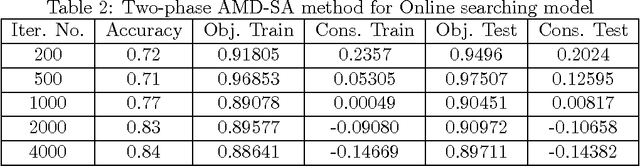
This paper considers the problem of minimizing an expectation function over a closed convex set, coupled with a functional or expectation constraint on either decision variables or problem parameters. We first present a new stochastic approximation (SA) type algorithm, namely the cooperative SA (CSA), to handle problems with the constraint on devision variables. We show that this algorithm exhibits the optimal O(1/\epsilon^2 ) rate of convergence, in terms of both optimality gap and constraint violation, when the objective and constraint functions are generally convex, where ? denotes the optimality gap and infeasibility. Moreover, we show that this rate of convergence can be improved to O(1/\epsilon) if the objective and constraint functions are strongly convex. We then present a variant of CSA, namely the cooperative stochastic parameter approximation (CSPA) algorithm, to deal with the situation when the constraint is defined over problem parameters and show that it exhibits similar optimal rate of convergence to CSA. It is worth noting that CSA and CSPA are primal methods which do not require the iterations on the dual space and/or the estimation on the size of the dual variables. To the best of our knowledge, this is the first time that such optimal SA methods for solving functional and expectation constrained stochastic optimization are presented in the literature.

Dynamic Stochastic Approximation for Multi-stage Stochastic Optimization

In this paper, we consider multi-stage stochastic optimization problems with convex objectives and conic constraints at each stage. We present a new stochastic first-order method, namely the dynamic stochastic approximation (DSA) algorithm, for solving these types of stochastic optimization problems. We show that DSA can achieve an optimal ${\cal O}(1/\epsilon^4)$ rate of convergence in terms of the total number of required scenarios when applied to a three-stage stochastic optimization problem. We further show that this rate of convergence can be improved to ${\cal O}(1/\epsilon^2)$ when the objective function is strongly convex. We also discuss variants of DSA for solving more general multi-stage stochastic optimization problems with the number of stages $T > 3$. The developed DSA algorithms only need to go through the scenario tree once in order to compute an $\epsilon$-solution of the multi-stage stochastic optimization problem. To the best of our knowledge, this is the first time that stochastic approximation type methods are generalized for multi-stage stochastic optimization with $T \ge 3$.