Complexity of normalized stochastic first-order methods with momentum under heavy-tailed noise

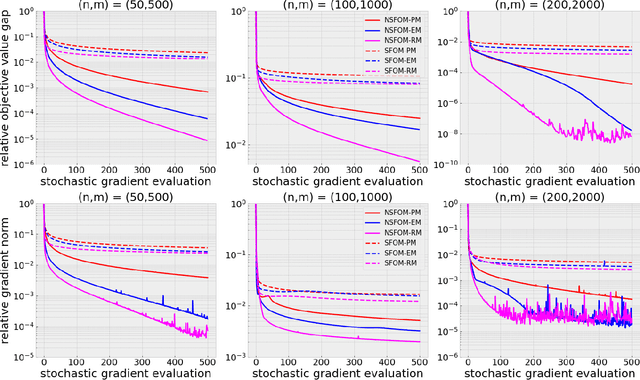
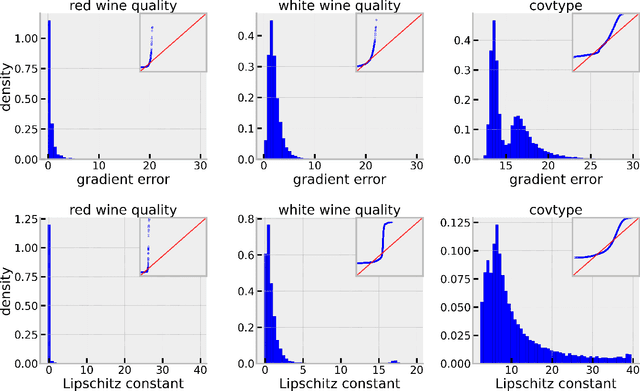
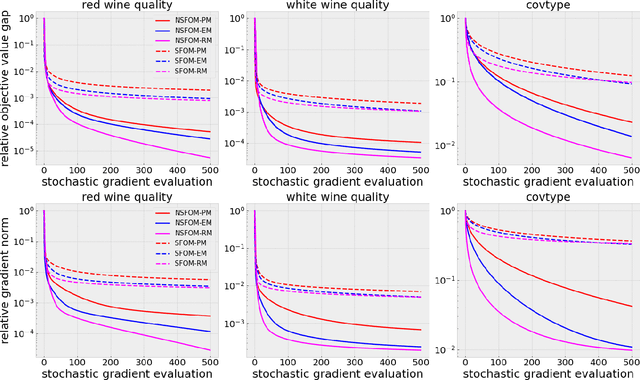
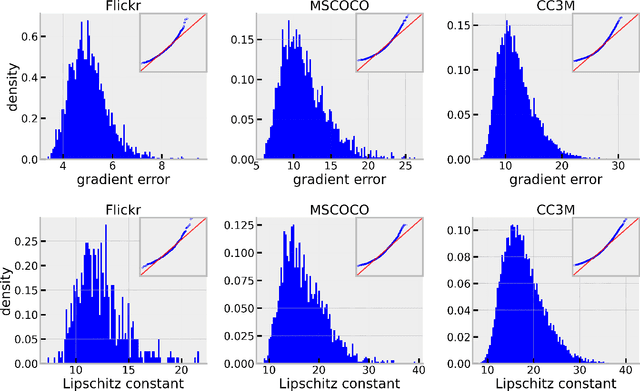
In this paper, we propose practical normalized stochastic first-order methods with Polyak momentum, multi-extrapolated momentum, and recursive momentum for solving unconstrained optimization problems. These methods employ dynamically updated algorithmic parameters and do not require explicit knowledge of problem-dependent quantities such as the Lipschitz constant or noise bound. We establish first-order oracle complexity results for finding approximate stochastic stationary points under heavy-tailed noise and weakly average smoothness conditions -- both of which are weaker than the commonly used bounded variance and mean-squared smoothness assumptions. Our complexity bounds either improve upon or match the best-known results in the literature. Numerical experiments are presented to demonstrate the practical effectiveness of the proposed methods.

Stochastic interior-point methods for smooth conic optimization with applications

Conic optimization plays a crucial role in many machine learning (ML) problems. However, practical algorithms for conic constrained ML problems with large datasets are often limited to specific use cases, as stochastic algorithms for general conic optimization remain underdeveloped. To fill this gap, we introduce a stochastic interior-point method (SIPM) framework for general conic optimization, along with four novel SIPM variants leveraging distinct stochastic gradient estimators. Under mild assumptions, we establish the global convergence rates of our proposed SIPMs, which, up to a logarithmic factor, match the best-known rates in stochastic unconstrained optimization. Finally, our numerical experiments on robust linear regression, multi-task relationship learning, and clustering data streams demonstrate the effectiveness and efficiency of our approach.