Blind denoising diffusion models and the blessings of dimensionality

We analyze, theoretically and empirically, the performance of generative diffusion models based on \emph{blind denoisers}, in which the denoiser is not given the noise amplitude in either the training or sampling processes. Assuming that the data distribution has low intrinsic dimensionality, we prove that blind denoising diffusion models (BDDMs), despite not having access to the noise amplitude, \emph{automatically} track a particular \emph{implicit} noise schedule along the reverse process. Our analysis shows that BDDMs can accurately sample from the data distribution in polynomially many steps as a function of the intrinsic dimension. Empirical results corroborate these mathematical findings on both synthetic and image data, demonstrating that the noise variance is accurately estimated from the noisy image. Remarkably, we observe that schedule-free BDDMs produce samples of higher quality compared to their non-blind counterparts. We provide evidence that this performance gain arises because BDDMs correct the mismatch between the true residual noise (of the image) and the noise assumed by the schedule used in non-blind diffusion models.

Learning normalized image densities via dual score matching

Learning probability models from data is at the heart of many machine learning endeavors, but is notoriously difficult due to the curse of dimensionality. We introduce a new framework for learning \emph{normalized} energy (log probability) models that is inspired from diffusion generative models, which rely on networks optimized to estimate the score. We modify a score network architecture to compute an energy while preserving its inductive biases. The gradient of this energy network with respect to its input image is the score of the learned density, which can be optimized using a denoising objective. Importantly, the gradient with respect to the noise level provides an additional score that can be optimized with a novel secondary objective, ensuring consistent and normalized energies across noise levels. We train an energy network with this \emph{dual} score matching objective on the ImageNet64 dataset, and obtain a cross-entropy (negative log likelihood) value comparable to the state of the art. We further validate our approach by showing that our energy model \emph{strongly generalizes}: estimated log probabilities are nearly independent of the specific images in the training set. Finally, we demonstrate that both image probability and dimensionality of local neighborhoods vary significantly with image content, in contrast with traditional assumptions such as concentration of measure or support on a low-dimensional manifold.

Feature-guided score diffusion for sampling conditional densities

Score diffusion methods can learn probability densities from samples. The score of the noise-corrupted density is estimated using a deep neural network, which is then used to iteratively transport a Gaussian white noise density to a target density. Variants for conditional densities have been developed, but correct estimation of the corresponding scores is difficult. We avoid these difficulties by introducing an algorithm that guides the diffusion with a projected score. The projection pushes the image feature vector towards the feature vector centroid of the target class. The projected score and the feature vectors are learned by the same network. Specifically, the image feature vector is defined as the spatial averages of the channels activations in select layers of the network. Optimizing the projected score for denoising loss encourages image feature vectors of each class to cluster around their centroids. It also leads to the separations of the centroids. We show that these centroids provide a low-dimensional Euclidean embedding of the class conditional densities. We demonstrate that the algorithm can generate high quality and diverse samples from the conditioning class. Conditional generation can be performed using feature vectors interpolated between those of the training set, demonstrating out-of-distribution generalization.

Optimized Linear Measurements for Inverse Problems using Diffusion-Based Image Generation

We re-examine the problem of reconstructing a high-dimensional signal from a small set of linear measurements, in combination with image prior from a diffusion probabilistic model. Well-established methods for optimizing such measurements include principal component analysis (PCA), independent component analysis (ICA) and compressed sensing (CS), all of which rely on axis- or subspace-aligned statistical characterization. But many naturally occurring signals, including photographic images, contain richer statistical structure. To exploit such structure, we introduce a general method for obtaining an optimized set of linear measurements, assuming a Bayesian inverse solution that leverages the prior implicit in a neural network trained to perform denoising. We demonstrate that these measurements are distinct from those of PCA and CS, with significant improvements in minimizing squared reconstruction error. In addition, we show that optimizing the measurements for the SSIM perceptual loss leads to perceptually improved reconstruction. Our results highlight the importance of incorporating the specific statistical regularities of natural signals when designing effective linear measurements.

Generalization in diffusion models arises from geometry-adaptive harmonic representation

High-quality samples generated with score-based reverse diffusion algorithms provide evidence that deep neural networks (DNN) trained for denoising can learn high-dimensional densities, despite the curse of dimensionality. However, recent reports of memorization of the training set raise the question of whether these networks are learning the "true" continuous density of the data. Here, we show that two denoising DNNs trained on non-overlapping subsets of a dataset learn nearly the same score function, and thus the same density, with a surprisingly small number of training images. This strong generalization demonstrates an alignment of powerful inductive biases in the DNN architecture and/or training algorithm with properties of the data distribution. We analyze these, demonstrating that the denoiser performs a shrinkage operation in a basis adapted to the underlying image. Examination of these bases reveals oscillating harmonic structures along contours and in homogeneous image regions. We show that trained denoisers are inductively biased towards these geometry-adaptive harmonic representations by demonstrating that they arise even when the network is trained on image classes such as low-dimensional manifolds, for which the harmonic basis is suboptimal. Additionally, we show that the denoising performance of the networks is near-optimal when trained on regular image classes for which the optimal basis is known to be geometry-adaptive and harmonic.

Learning multi-scale local conditional probability models of images

Deep neural networks can learn powerful prior probability models for images, as evidenced by the high-quality generations obtained with recent score-based diffusion methods. But the means by which these networks capture complex global statistical structure, apparently without suffering from the curse of dimensionality, remain a mystery. To study this, we incorporate diffusion methods into a multi-scale decomposition, reducing dimensionality by assuming a stationary local Markov model for wavelet coefficients conditioned on coarser-scale coefficients. We instantiate this model using convolutional neural networks (CNNs) with local receptive fields, which enforce both the stationarity and Markov properties. Global structures are captured using a CNN with receptive fields covering the entire (but small) low-pass image. We test this model on a dataset of face images, which are highly non-stationary and contain large-scale geometric structures. Remarkably, denoising, super-resolution, and image synthesis results all demonstrate that these structures can be captured with significantly smaller conditioning neighborhoods than required by a Markov model implemented in the pixel domain. Our results show that score estimation for large complex images can be reduced to low-dimensional Markov conditional models across scales, alleviating the curse of dimensionality.

Solving Linear Inverse Problems Using the Prior Implicit in a Denoiser

Prior probability models are a central component of many image processing problems, but density estimation is notoriously difficult for high-dimensional signals such as photographic images. Deep neural networks have provided state-of-the-art solutions for problems such as denoising, which implicitly rely on a prior probability model of natural images. Here, we develop a robust and general methodology for making use of this implicit prior. We rely on a little-known statistical result due to Miyasawa (1961), who showed that the least-squares solution for removing additive Gaussian noise can be written directly in terms of the gradient of the log of the noisy signal density. We use this fact to develop a stochastic coarse-to-fine gradient ascent procedure for drawing high-probability samples from the implicit prior embedded within a CNN trained to perform blind (i.e., unknown noise level) least-squares denoising. A generalization of this algorithm to constrained sampling provides a method for using the implicit prior to solve any linear inverse problem, with no additional training. We demonstrate this general form of transfer learning in multiple applications, using the same algorithm to produce high-quality solutions for deblurring, super-resolution, inpainting, and compressive sensing.

Robust and interpretable blind image denoising via bias-free convolutional neural networks

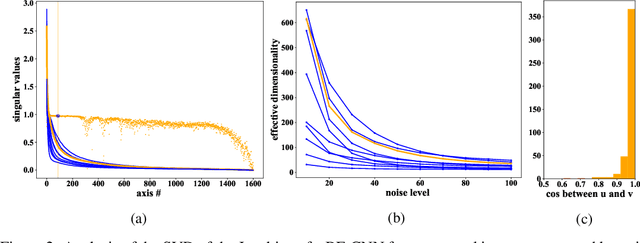
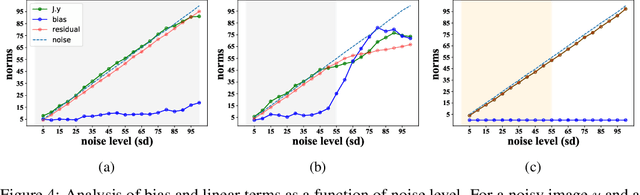
Deep convolutional networks often append additive constant ("bias") terms to their convolution operations, enabling a richer repertoire of functional mappings. Biases are also used to facilitate training, by subtracting mean response over batches of training images (a component of "batch normalization"). Recent state-of-the-art blind denoising methods (e.g., DnCNN) seem to require these terms for their success. Here, however, we show that these networks systematically overfit the noise levels for which they are trained: when deployed at noise levels outside the training range, performance degrades dramatically. In contrast, a bias-free architecture -- obtained by removing the constant terms in every layer of the network, including those used for batch normalization-- generalizes robustly across noise levels, while preserving state-of-the-art performance within the training range. Locally, the bias-free network acts linearly on the noisy image, enabling direct analysis of network behavior via standard linear-algebraic tools. These analyses provide interpretations of network functionality in terms of nonlinear adaptive filtering, and projection onto a union of low-dimensional subspaces, connecting the learning-based method to more traditional denoising methodology.