Agentic Meta-Orchestrator for Multi-task Copilots

Microsoft Copilot suites serve as the universal entry point for various agents skilled in handling important tasks, ranging from assisting a customer with product purchases to detecting vulnerabilities in corporate programming code. Each agent can be powered by language models, software engineering operations, such as database retrieval, and internal \& external knowledge. The repertoire of a copilot can expand dynamically with new agents. This requires a robust orchestrator that can distribute tasks from user prompts to the right agents. In this work, we propose an Agentic Meta-orchestrator (AMO) for handling multiple tasks and scalable agents in copilot services, which can provide both natural language and action responses. We will also demonstrate the planning that leverages meta-learning, i.e., a trained decision tree model for deciding the best inference strategy among various agents/models. We showcase the effectiveness of our AMO through two production use cases: Microsoft 365 (M365) E-Commerce Copilot and code compliance copilot. M365 E-Commerce Copilot advertises Microsoft products to external customers to promote sales success. The M365 E-Commerce Copilot provides up-to-date product information and connects to multiple agents, such as relational databases and human customer support. The code compliance copilot scans the internal DevOps code to detect known and new compliance issues in pull requests (PR).

Linear Constrained Rayleigh Quotient Optimization: Theory and Algorithms

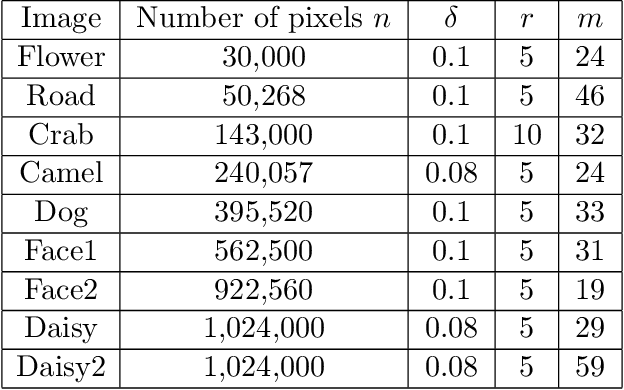
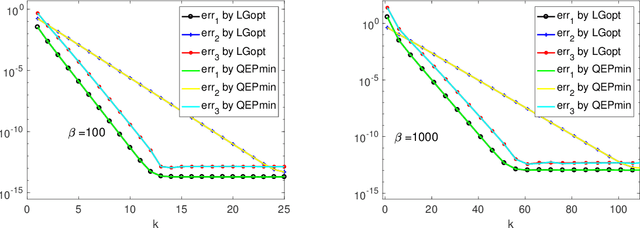
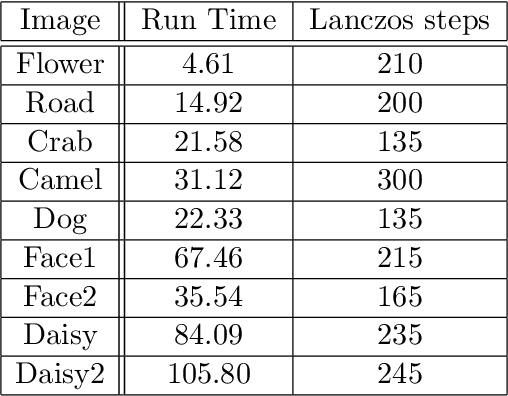
We consider the following constrained Rayleigh quotient optimization problem (CRQopt) $$ \min_{x\in \mathbb{R}^n} x^{T}Ax\,\,\mbox{subject to}\,\, x^{T}x=1\,\mbox{and}\,C^{T}x=b, $$ where $A$ is an $n\times n$ real symmetric matrix and $C$ is an $n\times m$ real matrix. Usually, $m\ll n$. The problem is also known as the constrained eigenvalue problem in the literature because it becomes an eigenvalue problem if the linear constraint $C^{T}x=b$ is removed. We start by equivalently transforming CRQopt into an optimization problem, called LGopt, of minimizing the Lagrangian multiplier of CRQopt, and then an problem, called QEPmin, of finding the smallest eigenvalue of a quadratic eigenvalue problem. Although such equivalences has been discussed in the literature, it appears to be the first time that these equivalences are rigorously justified. Then we propose to numerically solve LGopt and QEPmin by the Krylov subspace projection method via the Lanczos process. The basic idea, as the Lanczos method for the symmetric eigenvalue problem, is to first reduce LGopt and QEPmin by projecting them onto Krylov subspaces to yield problems of the same types but of much smaller sizes, and then solve the reduced problems by some direct methods, which is either a secular equation solver (in the case of LGopt) or an eigensolver (in the case of QEPmin). The resulting algorithm is called the Lanczos algorithm. We perform convergence analysis for the proposed method and obtain error bounds. The sharpness of the error bound is demonstrated by artificial examples, although in applications the method often converges much faster than the bounds suggest. Finally, we apply the Lanczos algorithm to semi-supervised learning in the context of constrained clustering.