Yun-Yang Liu
Fully-Connected Tensor Network Decomposition for Robust Tensor Completion Problem
Oct 17, 2021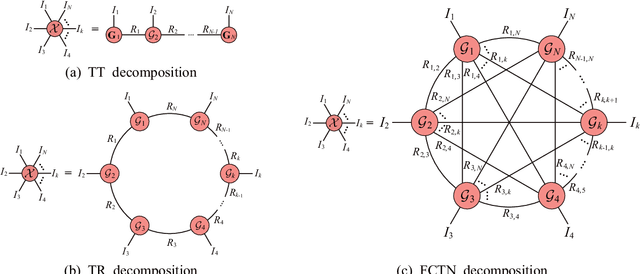
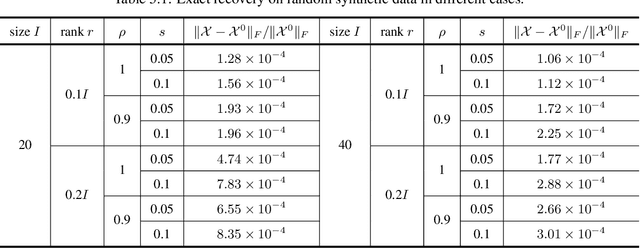
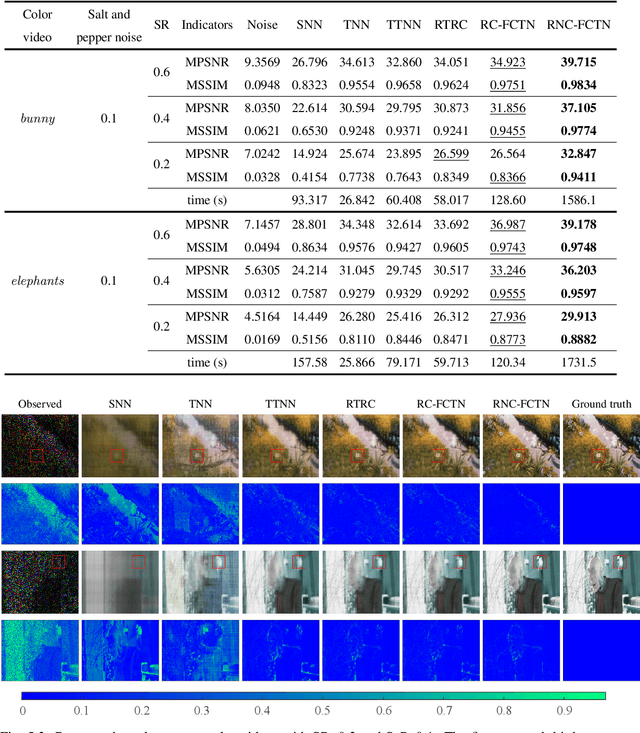
Abstract:The robust tensor completion (RTC) problem, which aims to reconstruct a low-rank tensor from partially observed tensor contaminated by a sparse tensor, has received increasing attention. In this paper, by leveraging the superior expression of the fully-connected tensor network (FCTN) decomposition, we propose a $\textbf{FCTN}$-based $\textbf{r}$obust $\textbf{c}$onvex optimization model (RC-FCTN) for the RTC problem. Then, we rigorously establish the exact recovery guarantee for the RC-FCTN. For solving the constrained optimization model RC-FCTN, we develop an alternating direction method of multipliers (ADMM)-based algorithm, which enjoys the global convergence guarantee. Moreover, we suggest a $\textbf{FCTN}$-based $\textbf{r}$obust $\textbf{n}$on$\textbf{c}$onvex optimization model (RNC-FCTN) for the RTC problem. A proximal alternating minimization (PAM)-based algorithm is developed to solve the proposed RNC-FCTN. Meanwhile, we theoretically derive the convergence of the PAM-based algorithm. Comprehensive numerical experiments in several applications, such as video completion and video background subtraction, demonstrate that proposed methods are superior to several state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge