Beyond Procrustes: Balancing-Free Gradient Descent for Asymmetric Low-Rank Matrix Sensing

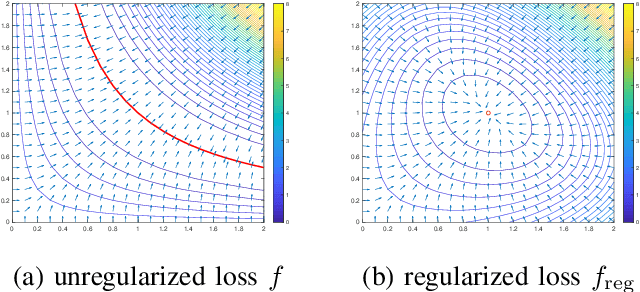
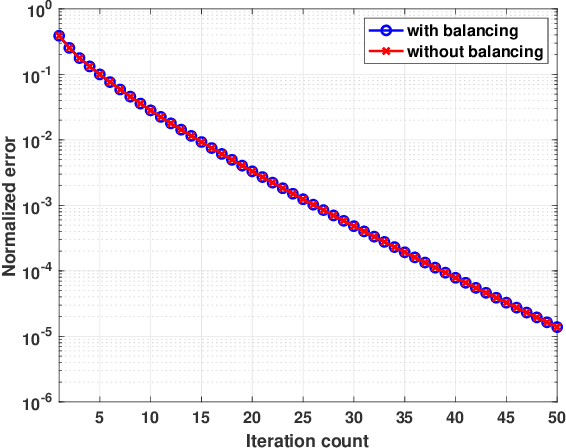
Low-rank matrix estimation plays a central role in various applications across science and engineering. Recently, nonconvex formulations based on matrix factorization are provably solved by simple gradient descent algorithms with strong computational and statistical guarantees. However, when the low-rank matrices are asymmetric, existing approaches rely on adding a regularization term to balance the scale of the two matrix factors which in practice can be removed safely without hurting the performance when initialized via the spectral method. In this paper, we provide a theoretical justification to this for the matrix sensing problem, which aims to recover a low-rank matrix from a small number of linear measurements. As long as the measurement ensemble satisfies the restricted isometry property, gradient descent -- in conjunction with spectral initialization -- converges linearly without the need of explicitly promoting balancedness of the factors; in fact, the factors stay balanced automatically throughout the execution of the algorithm. Our analysis is based on analyzing the evolution of a new distance metric that directly accounts for the ambiguity due to invertible transforms, and might be of independent interest.

Nonconvex Matrix Factorization from Rank-One Measurements

We consider the problem of recovering low-rank matrices from random rank-one measurements, which spans numerous applications including covariance sketching, phase retrieval, quantum state tomography, and learning shallow polynomial neural networks, among others. Our approach is to directly estimate the low-rank factor by minimizing a nonconvex quadratic loss function via vanilla gradient descent, following a tailored spectral initialization. When the true rank is small, this algorithm is guaranteed to converge to the ground truth (up to global ambiguity) with near-optimal sample complexity and computational complexity. To the best of our knowledge, this is the first guarantee that achieves near-optimality in both metrics. In particular, the key enabler of near-optimal computational guarantees is an implicit regularization phenomenon: without explicit regularization, both spectral initialization and the gradient descent iterates automatically stay within a region incoherent with the measurement vectors. This feature allows one to employ much more aggressive step sizes compared with the ones suggested in prior literature, without the need of sample splitting.

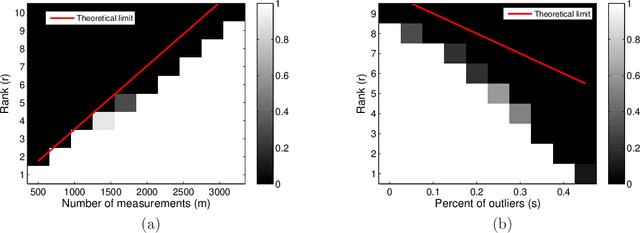
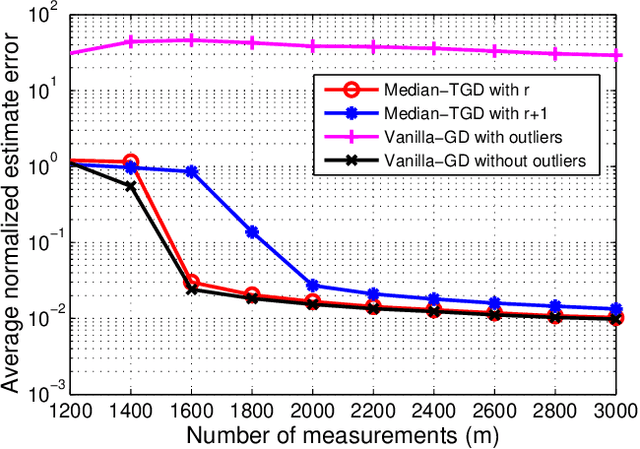
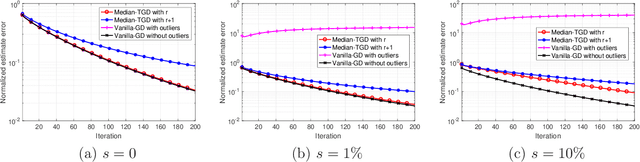
Nonconvex Low-Rank Matrix Recovery with Arbitrary Outliers via Median-Truncated Gradient Descent

Recent work has demonstrated the effectiveness of gradient descent for directly recovering the factors of low-rank matrices from random linear measurements in a globally convergent manner when initialized properly. However, the performance of existing algorithms is highly sensitive in the presence of outliers that may take arbitrary values. In this paper, we propose a truncated gradient descent algorithm to improve the robustness against outliers, where the truncation is performed to rule out the contributions of samples that deviate significantly from the {\em sample median} of measurement residuals adaptively in each iteration. We demonstrate that, when initialized in a basin of attraction close to the ground truth, the proposed algorithm converges to the ground truth at a linear rate for the Gaussian measurement model with a near-optimal number of measurements, even when a constant fraction of the measurements are arbitrarily corrupted. In addition, we propose a new truncated spectral method that ensures an initialization in the basin of attraction at slightly higher requirements. We finally provide numerical experiments to validate the superior performance of the proposed approach.