Function Forms of Simple ReLU Networks with Random Hidden Weights

We investigate the function space dynamics of a two-layer ReLU neural network in the infinite-width limit, highlighting the Fisher information matrix (FIM)'s role in steering learning. Extending seminal works on approximate eigendecomposition of the FIM, we derive the asymptotic behavior of basis functions ($f_v(x) = X^{\top} v $) for four groups of approximate eigenvectors, showing their convergence to distinct function forms. These functions, prioritized by gradient descent, exhibit FIM-induced inner products that approximate orthogonality in the function space, forging a novel connection between parameter and function spaces. Simulations validate the accuracy of these theoretical approximations, confirming their practical relevance. By refining the function space inner product's role, we advance the theoretical framework for ReLU networks, illuminating their optimization and expressivity. Overall, this work offers a robust foundation for understanding wide neural networks and enhances insights into scalable deep learning architectures, paving the way for improved design and analysis of neural networks.

Approximate Spectral Decomposition of Fisher Information Matrix for Simple ReLU Networks

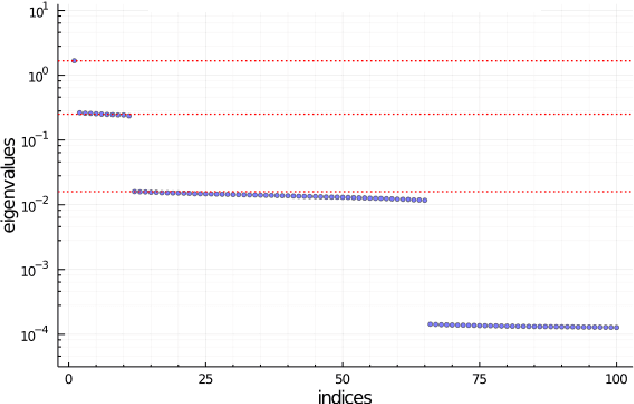
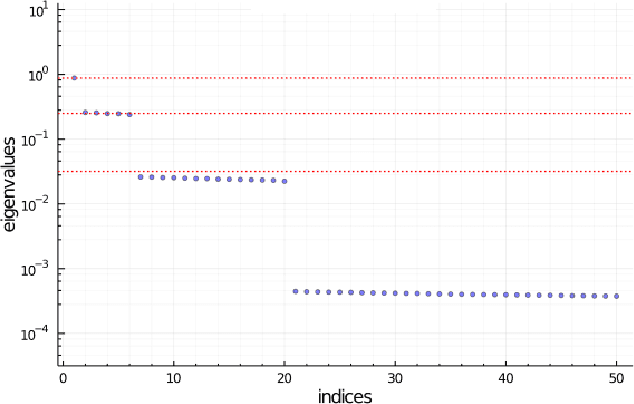
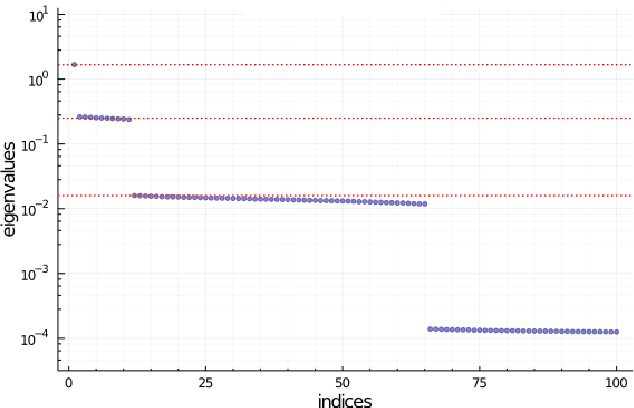
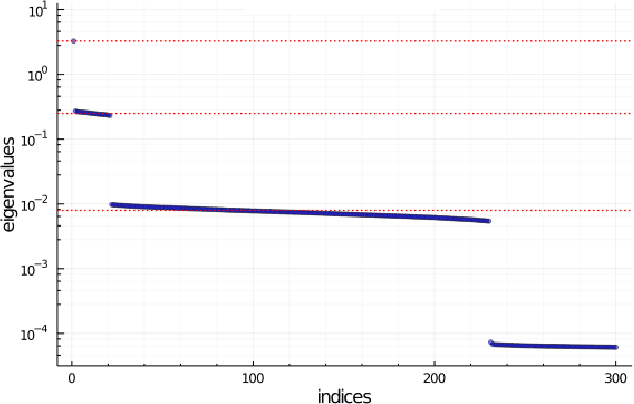
We investigate the Fisher information matrix (FIM) of one hidden layer networks with the ReLU activation function and obtain an approximate spectral decomposition of FIM under certain conditions. From this decomposition, we can approximate the main eigenvalues and eigenvectors. We confirmed by numerical simulation that the obtained decomposition is approximately correct when the number of hidden nodes is about 10000.