Sparsity via Hyperpriors: A Theoretical and Algorithmic Study under Empirical Bayes Framework

This paper presents a comprehensive analysis of hyperparameter estimation within the empirical Bayes framework (EBF) for sparse learning. By studying the influence of hyperpriors on the solution of EBF, we establish a theoretical connection between the choice of the hyperprior and the sparsity as well as the local optimality of the resulting solutions. We show that some strictly increasing hyperpriors, such as half-Laplace and half-generalized Gaussian with the power in $(0,1)$, effectively promote sparsity and improve solution stability with respect to measurement noise. Based on this analysis, we adopt a proximal alternating linearized minimization (PALM) algorithm with convergence guaranties for both convex and concave hyperpriors. Extensive numerical tests on two-dimensional image deblurring problems demonstrate that introducing appropriate hyperpriors significantly promotes the sparsity of the solution and enhances restoration accuracy. Furthermore, we illustrate the influence of the noise level and the ill-posedness of inverse problems to EBF solutions.

Sampling Strategies in Bayesian Inversion: A Study of RTO and Langevin Methods

This paper studies two classes of sampling methods for the solution of inverse problems, namely Randomize-Then-Optimize (RTO), which is rooted in sensitivity analysis, and Langevin methods, which are rooted in the Bayesian framework. The two classes of methods correspond to different assumptions and yield samples from different target distributions. We highlight the main conceptual and theoretical differences between the two approaches and compare them from a practical point of view by tackling two classical inverse problems in imaging: deblurring and inpainting. We show that the choice of the sampling method has a significant impact on the quality of the reconstruction and that the RTO method is more robust to the choice of the parameters.

A fast method for simultaneous reconstruction and segmentation in X-ray CT application

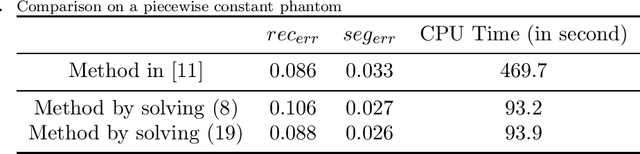
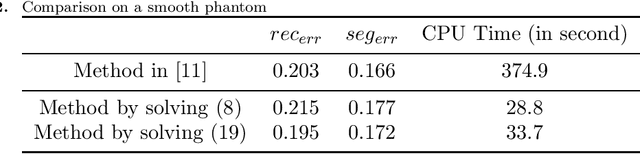
In this paper, we propose a fast method for simultaneous reconstruction and segmentation (SRS) in X-ray computed tomography (CT). Our work is based on the SRS model where Bayes' rule and the maximum a posteriori (MAP) are used on hidden Markov measure field model (HMMFM). The original method leads to a logarithmic-summation (log-sum) term, which is non-separable to the classification index. The minimization problem in the model was solved by using constrained gradient descend method, Frank-Wolfe algorithm, which is very time-consuming especially when dealing with large-scale CT problems. The starting point of this paper is the commutativity of log-sum operations, where the log-sum problem could be transformed into a sum-log problem by introducing an auxiliary variable. The corresponding sum-log problem for the SRS model is separable. After applying alternating minimization method, this problem turns into several easy-to-solve convex sub-problems. In the paper, we also study an improved model by adding Tikhonov regularization, and give some convergence results. Experimental results demonstrate that the proposed algorithms could produce comparable results with the original SRS method with much less CPU time.