Learning to Charge More: A Theoretical Study of Collusion by Q-Learning Agents

There is growing experimental evidence that $Q$-learning agents may learn to charge supracompetitive prices. We provide the first theoretical explanation for this behavior in infinite repeated games. Firms update their pricing policies based solely on observed profits, without computing equilibrium strategies. We show that when the game admits both a one-stage Nash equilibrium price and a collusive-enabling price, and when the $Q$-function satisfies certain inequalities at the end of experimentation, firms learn to consistently charge supracompetitive prices. We introduce a new class of one-memory subgame perfect equilibria (SPEs) and provide conditions under which learned behavior is supported by naive collusion, grim trigger policies, or increasing strategies. Naive collusion does not constitute an SPE unless the collusive-enabling price is a one-stage Nash equilibrium, whereas grim trigger policies can.

Artificial Intelligence and Algorithmic Price Collusion in Two-sided Markets

Algorithmic price collusion facilitated by artificial intelligence (AI) algorithms raises significant concerns. We examine how AI agents using Q-learning engage in tacit collusion in two-sided markets. Our experiments reveal that AI-driven platforms achieve higher collusion levels compared to Bertrand competition. Increased network externalities significantly enhance collusion, suggesting AI algorithms exploit them to maximize profits. Higher user heterogeneity or greater utility from outside options generally reduce collusion, while higher discount rates increase it. Tacit collusion remains feasible even at low discount rates. To mitigate collusive behavior and inform potential regulatory measures, we propose incorporating a penalty term in the Q-learning algorithm.

The effect of Leaky ReLUs on the training and generalization of overparameterized networks

We investigate the training and generalization errors of overparameterized neural networks (NNs) with a wide class of leaky rectified linear unit (ReLU) functions. More specifically, we carefully upper bound both the convergence rate of the training error and the generalization error of such NNs and investigate the dependence of these bounds on the Leaky ReLU parameter, $\alpha$. We show that $\alpha =-1$, which corresponds to the absolute value activation function, is optimal for the training error bound. Furthermore, in special settings, it is also optimal for the generalization error bound. Numerical experiments empirically support the practical choices guided by the theory.

An Unpooling Layer for Graph Generation

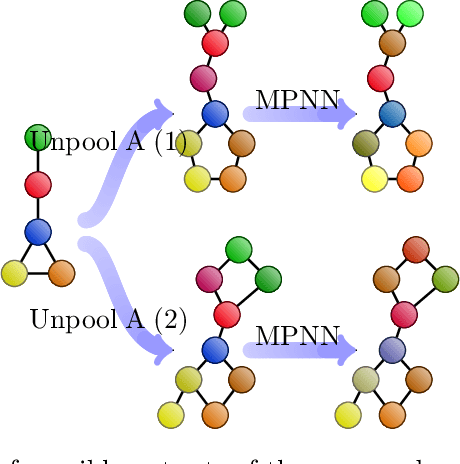
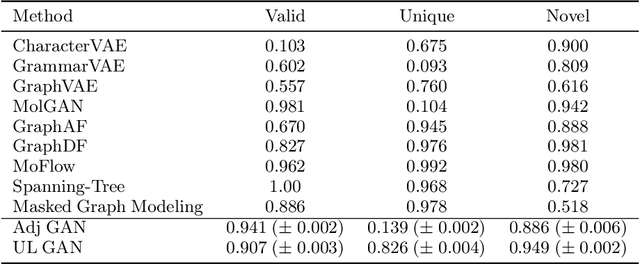
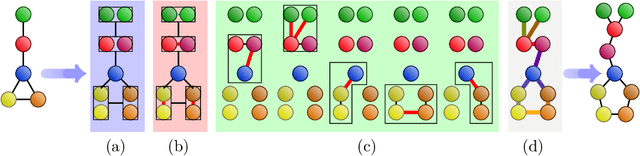
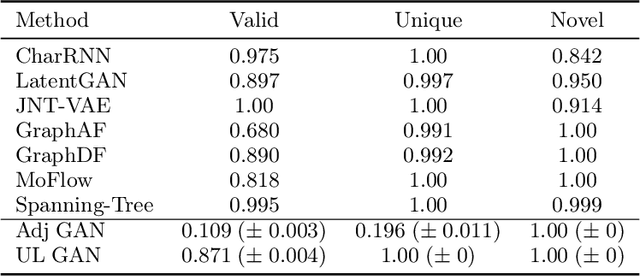
We propose a novel and trainable graph unpooling layer for effective graph generation. Given a graph with features, the unpooling layer enlarges this graph and learns its desired new structure and features. Since this unpooling layer is trainable, it can be applied to graph generation either in the decoder of a variational autoencoder or in the generator of a generative adversarial network (GAN). We prove that the unpooled graph remains connected and any connected graph can be sequentially unpooled from a 3-nodes graph. We apply the unpooling layer within the GAN generator. Since the most studied instance of graph generation is molecular generation, we test our ideas in this context. Using the QM9 and ZINC datasets, we demonstrate the improvement obtained by using the unpooling layer instead of an adjacency-matrix-based approach.