Asymptotic Behavior of Adversarial Training Estimator under $\ell_\infty$-Perturbation

Adversarial training has been proposed to hedge against adversarial attacks in machine learning and statistical models. This paper focuses on adversarial training under $\ell_\infty$-perturbation, which has recently attracted much research attention. The asymptotic behavior of the adversarial training estimator is investigated in the generalized linear model. The results imply that the limiting distribution of the adversarial training estimator under $\ell_\infty$-perturbation could put a positive probability mass at $0$ when the true parameter is $0$, providing a theoretical guarantee of the associated sparsity-recovery ability. Alternatively, a two-step procedure is proposed -- adaptive adversarial training, which could further improve the performance of adversarial training under $\ell_\infty$-perturbation. Specifically, the proposed procedure could achieve asymptotic unbiasedness and variable-selection consistency. Numerical experiments are conducted to show the sparsity-recovery ability of adversarial training under $\ell_\infty$-perturbation and to compare the empirical performance between classic adversarial training and adaptive adversarial training.

Adjusted Wasserstein Distributionally Robust Estimator in Statistical Learning

We propose an adjusted Wasserstein distributionally robust estimator -- based on a nonlinear transformation of the Wasserstein distributionally robust (WDRO) estimator in statistical learning. This transformation will improve the statistical performance of WDRO because the adjusted WDRO estimator is asymptotically unbiased and has an asymptotically smaller mean squared error. The adjusted WDRO will not mitigate the out-of-sample performance guarantee of WDRO. Sufficient conditions for the existence of the adjusted WDRO estimator are presented, and the procedure for the computation of the adjusted WDRO estimator is given. Specifically, we will show how the adjusted WDRO estimator is developed in the generalized linear model. Numerical experiments demonstrate the favorable practical performance of the adjusted estimator over the classic one.

Improved Rate of First Order Algorithms for Entropic Optimal Transport

This paper improves the state-of-the-art rate of a first-order algorithm for solving entropy regularized optimal transport. The resulting rate for approximating the optimal transport (OT) has been improved from $\widetilde{{O}}({n^{2.5}}/{\epsilon})$ to $\widetilde{{O}}({n^2}/{\epsilon})$, where $n$ is the problem size and $\epsilon$ is the accuracy level. In particular, we propose an accelerated primal-dual stochastic mirror descent algorithm with variance reduction. Such special design helps us improve the rate compared to other accelerated primal-dual algorithms. We further propose a batch version of our stochastic algorithm, which improves the computational performance through parallel computing. To compare, we prove that the computational complexity of the Stochastic Sinkhorn algorithm is $\widetilde{{O}}({n^2}/{\epsilon^2})$, which is slower than our accelerated primal-dual stochastic mirror algorithm. Experiments are done using synthetic and real data, and the results match our theoretical rates. Our algorithm may inspire more research to develop accelerated primal-dual algorithms that have rate $\widetilde{{O}}({n^2}/{\epsilon})$ for solving OT.

Solving a Special Type of Optimal Transport Problem by a Modified Hungarian Algorithm

We observe that computing empirical Wasserstein distance in the independence test is an optimal transport (OT) problem with a special structure. This observation inspires us to study a special type of OT problem and propose a modified Hungarian algorithm to solve it exactly. For an OT problem between marginals with $m$ and $n$ atoms ($m\geq n$), the computational complexity of the proposed algorithm is $O(m^2n)$. Computing the empirical Wasserstein distance in the independence test requires solving this special type of OT problem, where we have $m=n^2$. The associate computational complexity of our algorithm is $O(n^5)$, while the order of applying the classic Hungarian algorithm is $O(n^6)$. Numerical experiments validate our theoretical analysis. Broader applications of the proposed algorithm are discussed at the end.

An Accelerated Stochastic Algorithm for Solving the Optimal Transport Problem

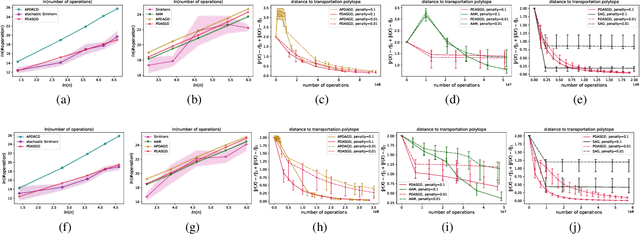
We propose a novel accelerated stochastic algorithm -- primal-dual accelerated stochastic gradient descent with variance reduction (PDASGD) -- for solving the optimal transport (OT) problem between two discrete distributions. PDASGD can also be utilized to compute for the Wasserstein barycenter (WB) of multiple discrete distributions. In both the OT and WB cases, the proposed algorithm enjoys the best-known convergence rate (in the form of order of computational complexity) in the literature. PDASGD is easy to implement in nature, due to its stochastic property: computation per iteration can be much faster than other non-stochastic counterparts. We carry out numerical experiments on both synthetic and real data; they demonstrate the improved efficiency of PDASGD.