Going from a Representative Agent to Counterfactuals in Combinatorial Choice

We study decision-making problems where data comprises points from a collection of binary polytopes, capturing aggregate information stemming from various combinatorial selection environments. We propose a nonparametric approach for counterfactual inference in this setting based on a representative agent model, where the available data is viewed as arising from maximizing separable concave utility functions over the respective binary polytopes. Our first contribution is to precisely characterize the selection probabilities representable under this model and show that verifying the consistency of any given aggregated selection dataset reduces to solving a polynomial-sized linear program. Building on this characterization, we develop a nonparametric method for counterfactual prediction. When data is inconsistent with the model, finding a best-fitting approximation for prediction reduces to solving a compact mixed-integer convex program. Numerical experiments based on synthetic data demonstrate the method's flexibility, predictive accuracy, and strong representational power even under model misspecification.

The Limit of the Marginal Distribution Model in Consumer Choice

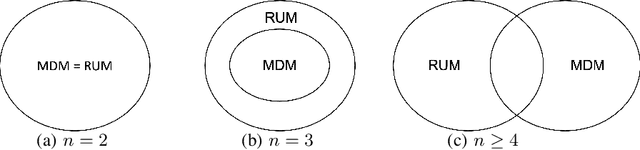
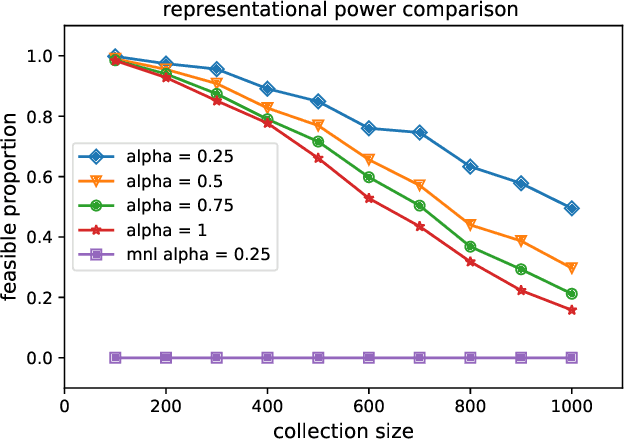
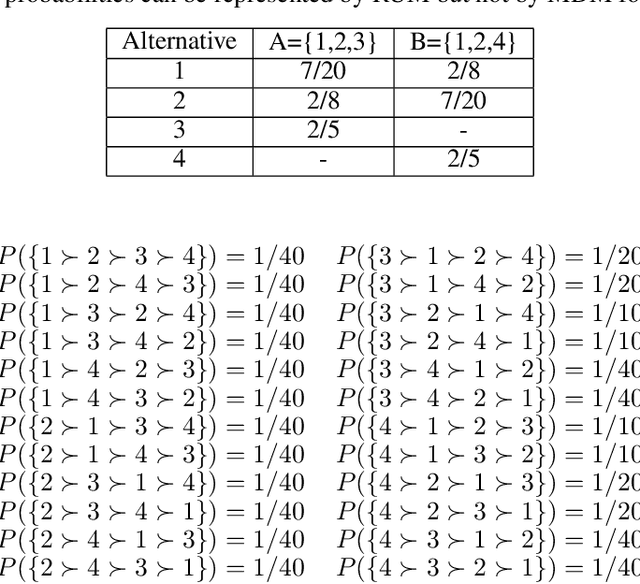
Given data on choices made by consumers for different assortments, a key challenge is to develop parsimonious models that describe and predict consumer choice behavior. One such choice model is the marginal distribution model which requires only the specification of the marginal distributions of the random utilities of the alternatives to explain choice data. In this paper, we develop an exact characterisation of the set of choice probabilities which are representable by the marginal distribution model consistently across any collection of assortments. Allowing for the possibility of alternatives to be grouped based on the marginal distribution of their utilities, we show (a) verifying consistency of choice probability data with this model is possible in polynomial time and (b) finding the closest fit reduces to solving a mixed integer convex program. Our results show that the marginal distribution model provides much better representational power as compared to multinomial logit and much better computational performance as compared to the random utility model.