Consensus Sampling for Safer Generative AI

Many approaches to AI safety rely on inspecting model outputs or activations, yet certain risks are inherently undetectable by inspection alone. We propose a complementary, architecture-agnostic approach that enhances safety through the aggregation of multiple generative models, with the aggregated model inheriting its safety from the safest subset of a given size among them. Specifically, we present a consensus sampling algorithm that, given $k$ models and a prompt, achieves risk competitive with the average risk of the safest $s$ of the $k$ models, where $s$ is a chosen parameter, while abstaining when there is insufficient agreement between them. The approach leverages the models' ability to compute output probabilities, and we bound the probability of abstention when sufficiently many models are safe and exhibit adequate agreement. The algorithm is inspired by the provable copyright protection algorithm of Vyas et al. (2023). It requires some overlap among safe models, offers no protection when all models are unsafe, and may accumulate risk over repeated use. Nonetheless, our results provide a new, model-agnostic approach for AI safety by amplifying safety guarantees from an unknown subset of models within a collection to that of a single reliable model.

Beyond Perturbations: Learning Guarantees with Arbitrary Adversarial Test Examples

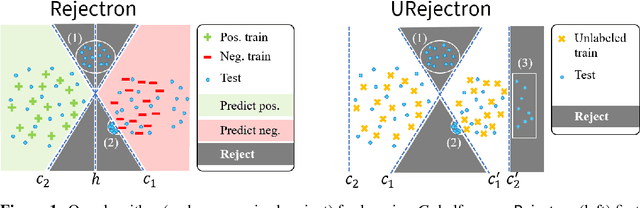
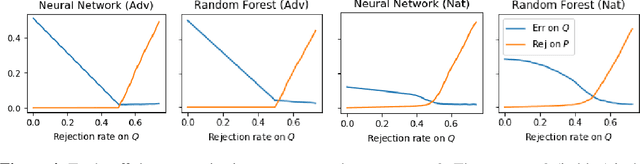
We present a transductive learning algorithm that takes as input training examples from a distribution $P$ and arbitrary (unlabeled) test examples, possibly chosen by an adversary. This is unlike prior work that assumes that test examples are small perturbations of $P$. Our algorithm outputs a selective classifier, which abstains from predicting on some examples. By considering selective transductive learning, we give the first nontrivial guarantees for learning classes of bounded VC dimension with arbitrary train and test distributions---no prior guarantees were known even for simple classes of functions such as intervals on the line. In particular, for any function in a class $C$ of bounded VC dimension, we guarantee a low test error rate and a low rejection rate with respect to $P$. Our algorithm is efficient given an Empirical Risk Minimizer (ERM) for $C$. Our guarantees hold even for test examples chosen by an unbounded white-box adversary. We also give guarantees for generalization, agnostic, and unsupervised settings.