Learning When-to-Treat Policies

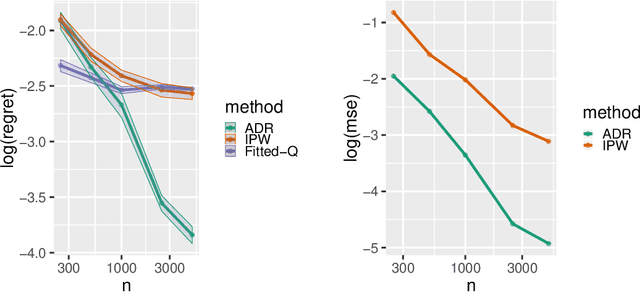
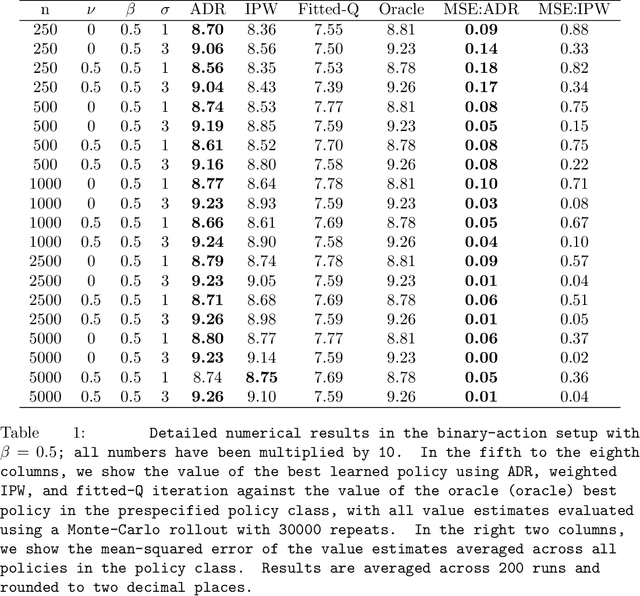
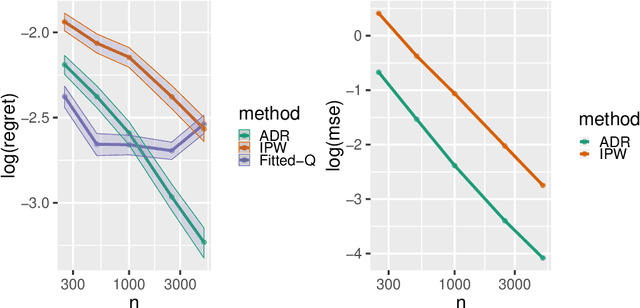
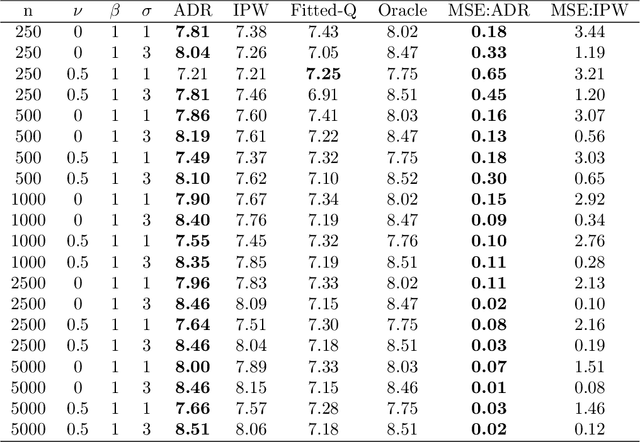
Many applied decision-making problems have a dynamic component: The policymaker needs not only to choose whom to treat, but also when to start which treatment. For example, a medical doctor may see a patient many times and, at each visit, need to choose between prescribing either an invasive or a non-invasive procedure and postponing the decision to the next visit. In this paper, we develop an \say{advantage doubly robust} estimator for learning such dynamic treatment rules using observational data under sequential ignorability. We prove welfare regret bounds that generalize results for doubly robust learning in the single-step setting, and show promising empirical performance in several different contexts. Our approach is practical for policy optimization, and does not need any structural (e.g., Markovian) assumptions.

Quasi-Oracle Estimation of Heterogeneous Treatment Effects

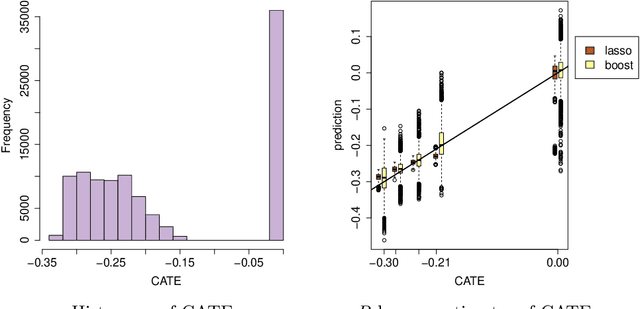
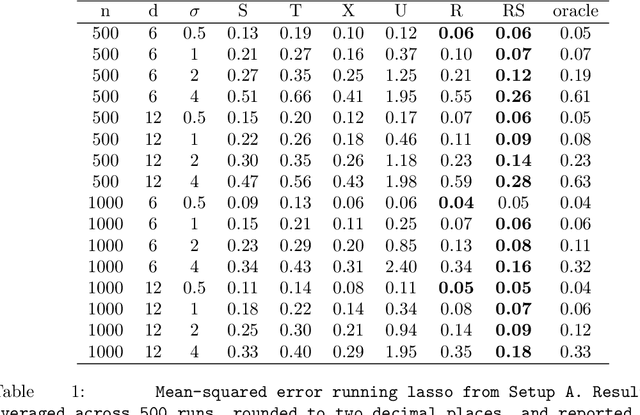
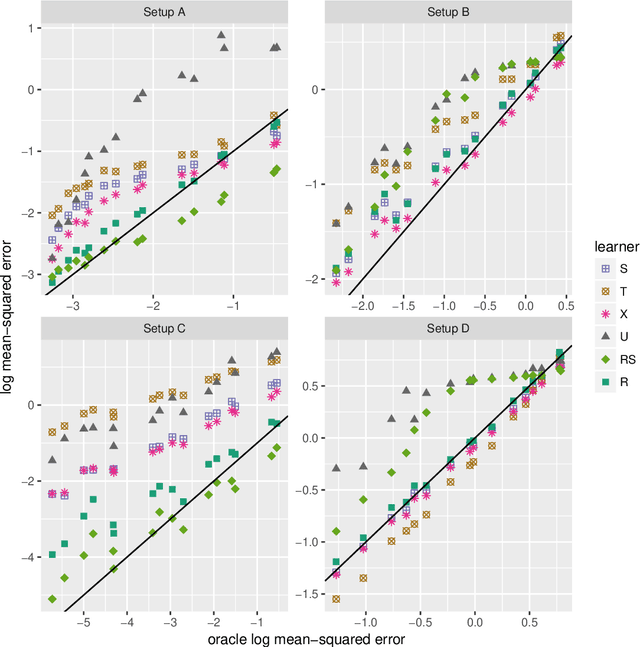
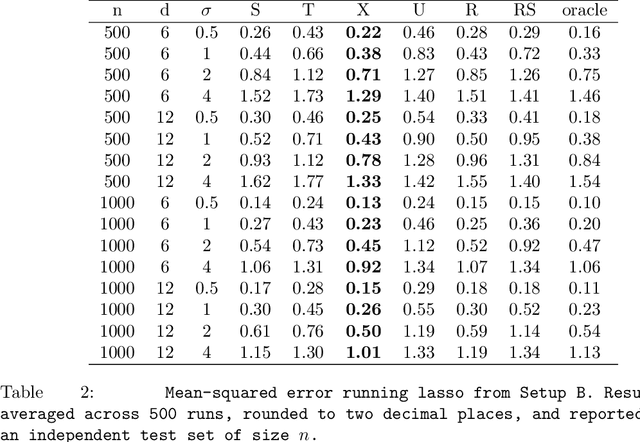
Flexible estimation of heterogeneous treatment effects lies at the heart of many statistical challenges, such as personalized medicine and optimal resource allocation. In this paper, we develop a general class of two-step algorithms for heterogeneous treatment effect estimation in observational studies. We first estimate marginal effects and treatment propensities in order to form an objective function that isolates the causal component of the signal. Then, we optimize this data-adaptive objective function. Our approach has several advantages over existing methods. From a practical perspective, our method is flexible and easy to use: For both steps, we can use any loss-minimization method, e.g., penalized regression, deep neutral networks, or boosting; moreover, these methods can be fine-tuned by cross validation. Meanwhile, in the case of penalized kernel regression, we show that our method has a quasi-oracle property: Even if the pilot estimates for marginal effects and treatment propensities are not particularly accurate, we achieve the same regret bounds as an oracle who has a priori knowledge of these two nuisance components. We implement variants of our approach based on both penalized regression and boosting in a variety of simulation setups, and find promising performance relative to existing baselines.

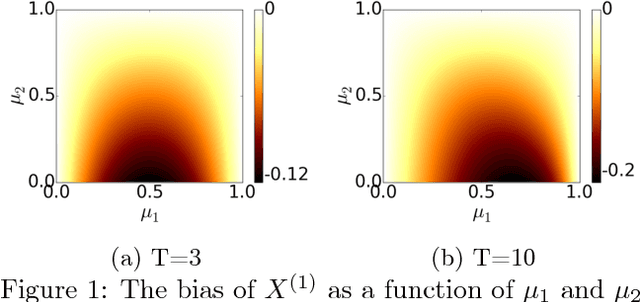
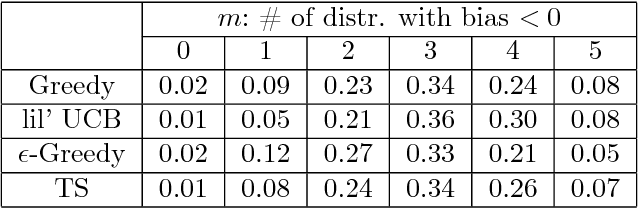
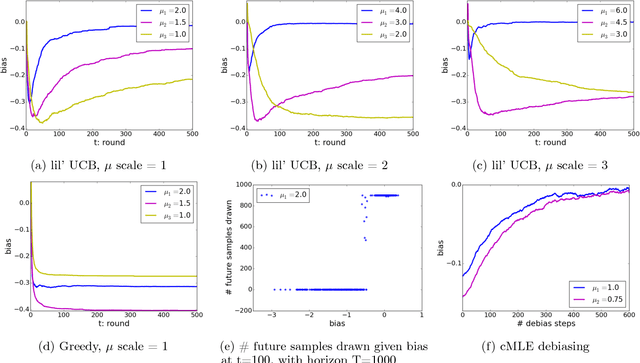
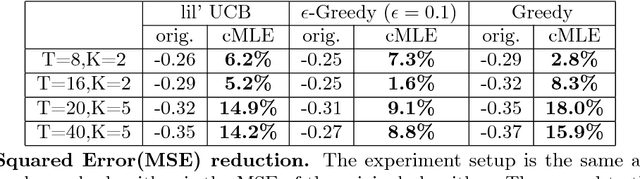
Why Adaptively Collected Data Have Negative Bias and How to Correct for It

From scientific experiments to online A/B testing, the previously observed data often affects how future experiments are performed, which in turn affects which data will be collected. Such adaptivity introduces complex correlations between the data and the collection procedure. In this paper, we prove that when the data collection procedure satisfies natural conditions, then sample means of the data have systematic \emph{negative} biases. As an example, consider an adaptive clinical trial where additional data points are more likely to be tested for treatments that show initial promise. Our surprising result implies that the average observed treatment effects would underestimate the true effects of each treatment. We quantitatively analyze the magnitude and behavior of this negative bias in a variety of settings. We also propose a novel debiasing algorithm based on selective inference techniques. In experiments, our method can effectively reduce bias and estimation error.