Extended Spherical Geometry Algorithm for Spaceborne SAR Processing in Stripmap and TOPS Imaging Modes

The Spherical Geometry Algorithm (SGA) demonstrates superior capability in achieving efficient and precise spaceborne SAR image formation processing, even under challenging imaging conditions including non-linear radar trajectories and spherical Earth surface geometry. Nevertheless, the original SGA is specifically developed for spotlight SAR data processing and can't directly applied to processing spaceborne SAR data in other modes. In this paper, we first analyze the limitations of the SGA algorithm when applied to stripmap or TOPS mode SAR processing, and then propose an improved SGA algorithm which can process both stripmap and TOPS SAR data. Compared with the original algorithm, the new algorithm has two main differences. Firstly, in order to avoid undersampling during azimuth resampling in both modes, an instantaneous Doppler centroid removal process was added before azimuth interpolation processing by exploiting the endomorphism property of resampling operation. Secondly, the spectral analysis method used for the final step of azimuth compression in the original SGA has been replaced with a new matched filtering processing, which can avoid image aliasing in azimuth direction and improve computational efficiency. Measured real data processing results are presented to demonstrate the validity of the proposed algorithms.

Spherical Geometry Algorithm for Space-borne Synthetic Aperture Radar Imaging

Higher spatial resolution and larger imaging scene are always the goals pursued by advanced space-borne SAR system.High resolution and wide swath SAR imaging can provide more information about the illuminated scene of interest on one hand,but also come with some new challenges on the other hand.The induced new challenging problems include curved orbit,Earth rotation,and spherical ground surface,etc.Most existing image formation algorithms suffer from performance deficiency in these challenging cases,either in focus accuracy or computational efficiency.In this paper,an accurate Fourier transform relationship between the phase history domain data and the scene reflectivity function is derived under arbitrary radar trajectory by exploiting the spherical geometry property of the space-borne SAR data collection.Using the derived new data model,an image reconstruction algorithm based on Fourier inversion is proposed.The new algorithm has the inherent capability of correcting for the curved orbit and spherical ground surface effect.Meanwhile,the out-of-plane motion effect induced by the Earth's rotation can also be compensated by a two-step phase correction and data projection procedure embedded in the Fourier inversion reconstruction.The new algorithm inherits the merit of both time domain and frequency domain algorithms,has excellent performance in both focus accuracy and computational efficiency.Both simulation and real data processing results validate the effectiveness of the proposed imaging algorithm.

SAR Imaging of Moving Target based on Knowledge-aided Two-dimensional Autofocus

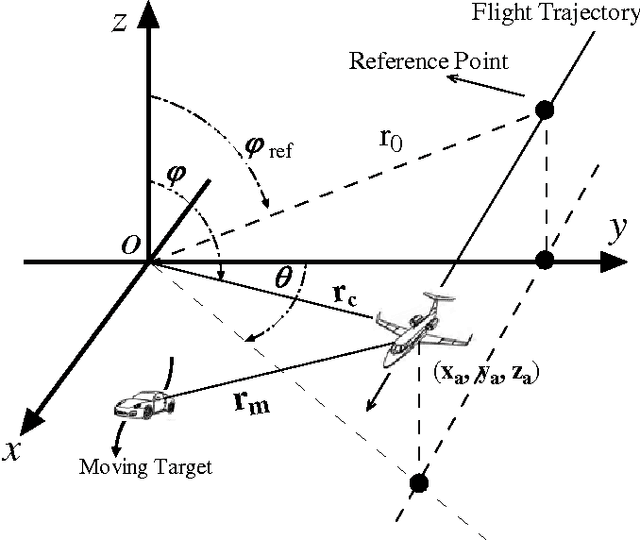
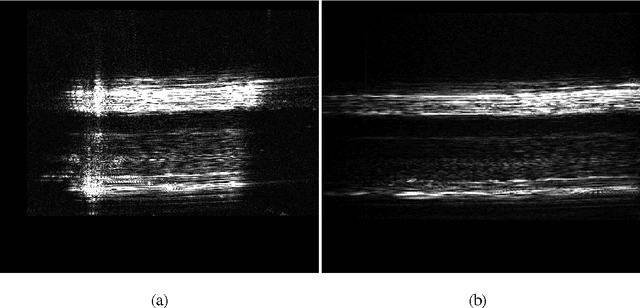
Due to uncertainty on target's motion, the range cell migration (RCM) and azimuth phase error (APE) of moving targets can't be completely compensated in synthetic aperture radar (SAR) processing. Therefore, moving targets often appear two-dimensional (2-D) defocused in SAR images. In this paper, a 2-D autofocus method for refocusing defocused moving targets in SAR images is presented. The new method only requires a direct estimate of APE, while the residual 2-D phase error ( or RCM) is computed from the estimated APE by exploiting the analytical relationship between the 2-D phase error ( or RCM) and APE. Because the parameter estimation is performed in the reduced-dimension space by exploiting prior knowledge on phase error structure, the proposed approach offers clear advantages in both computational efficiency and estimation accuracy.

Autofocus Correction of Azimuth Phase Error and Residual Range Cell Migration in Spotlight SAR Polar Format Imagery

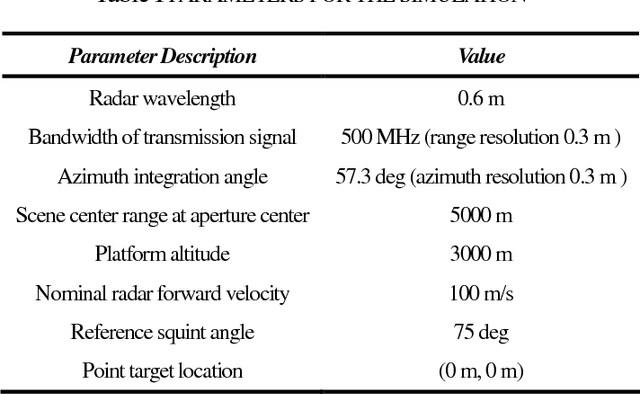
Synthetic aperture radar (SAR) images are often blurred by phase perturbations induced by uncompensated sensor motion and /or unknown propagation effects caused by turbulent media. To get refocused images, autofocus proves to be useful post-processing technique applied to estimate and compensate the unknown phase errors. However, a severe drawback of the conventional autofocus algorithms is that they are only capable of removing one-dimensional azimuth phase errors (APE). As the resolution becomes finer, residual range cell migration (RCM), which makes the defocus inherently two-dimensional, becomes a new challenge. In this paper, correction of APE and residual RCM are presented in the framework of polar format algorithm (PFA). First, an insight into the underlying mathematical mechanism of polar reformatting is presented. Then based on this new formulation, the effect of polar reformatting on the uncompensated APE and residual RCM is investigated in detail. By using the derived analytical relationship between APE and residual RCM, an efficient two-dimensional (2-D) autofocus method is proposed. Experimental results indicate the effectiveness of the proposed method.