Xingjie Li
ISALT: Inference-based schemes adaptive to large time-stepping for locally Lipschitz ergodic systems
Feb 25, 2021
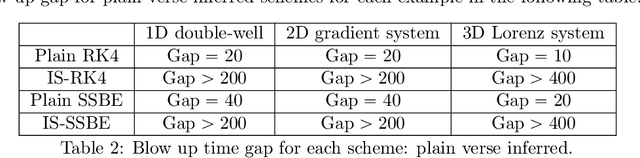
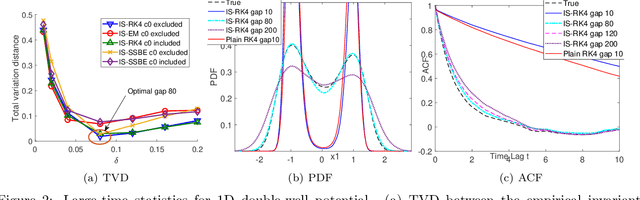
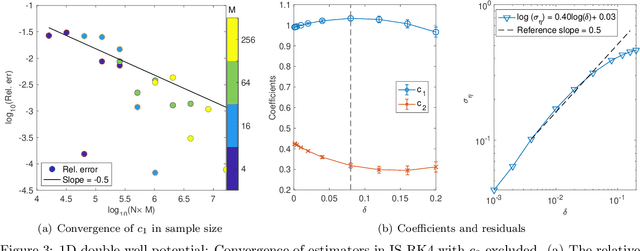
Abstract:Efficient simulation of SDEs is essential in many applications, particularly for ergodic systems that demand efficient simulation of both short-time dynamics and large-time statistics. However, locally Lipschitz SDEs often require special treatments such as implicit schemes with small time-steps to accurately simulate the ergodic measure. We introduce a framework to construct inference-based schemes adaptive to large time-steps (ISALT) from data, achieving a reduction in time by several orders of magnitudes. The key is the statistical learning of an approximation to the infinite-dimensional discrete-time flow map. We explore the use of numerical schemes (such as the Euler-Maruyama, a hybrid RK4, and an implicit scheme) to derive informed basis functions, leading to a parameter inference problem. We introduce a scalable algorithm to estimate the parameters by least squares, and we prove the convergence of the estimators as data size increases. We test the ISALT on three non-globally Lipschitz SDEs: the 1D double-well potential, a 2D multi-scale gradient system, and the 3D stochastic Lorenz equation with degenerate noise. Numerical results show that ISALT can tolerate time-step magnitudes larger than plain numerical schemes. It reaches optimal accuracy in reproducing the invariant measure when the time-step is medium-large.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge