How Well Can AI Build SD Models?

Introduction: As system dynamics (SD) embraces automation, AI offers efficiency but risks bias from missing data and flawed models. Models that omit multiple perspectives and data threaten model quality, whether created by humans or with the assistance of AI. To reduce uncertainty about how well AI can build SD models, we introduce two metrics for evaluation of AI-generated causal maps: technical correctness (causal translation) and adherence to instructions (conformance). Approach: We developed an open source project called sd-ai to provide a basis for collaboration in the SD community, aiming to fully harness the potential of AI based tools like ChatGPT for dynamic modeling. Additionally, we created an evaluation theory along with a comprehensive suite of tests designed to evaluate any such tools developed within the sd-ai ecosystem. Results: We tested 11 different LLMs on their ability to do causal translation as well as conform to user instruction. gpt-4.5-preview was the top performer, scoring 92.9% overall, excelling in both tasks. o1 scored 100% in causal translation. gpt-4o identified all causal links but struggled with positive polarity in decreasing terms. While gpt-4.5-preview and o1 are most accurate, gpt-4o is the cheapest. Discussion: Causal translation and conformance tests applied to the sd-ai engine reveal significant variations across lLLMs, underscoring the need for continued evaluation to ensure responsible development of AI tools for dynamic modeling. To address this, an open collaboration among tool developers, modelers, and stakeholders is launched to standardize measures for evaluating the capacity of AI tools to improve the modeling process.

Automated Diagram Generation to Build Understanding and Usability

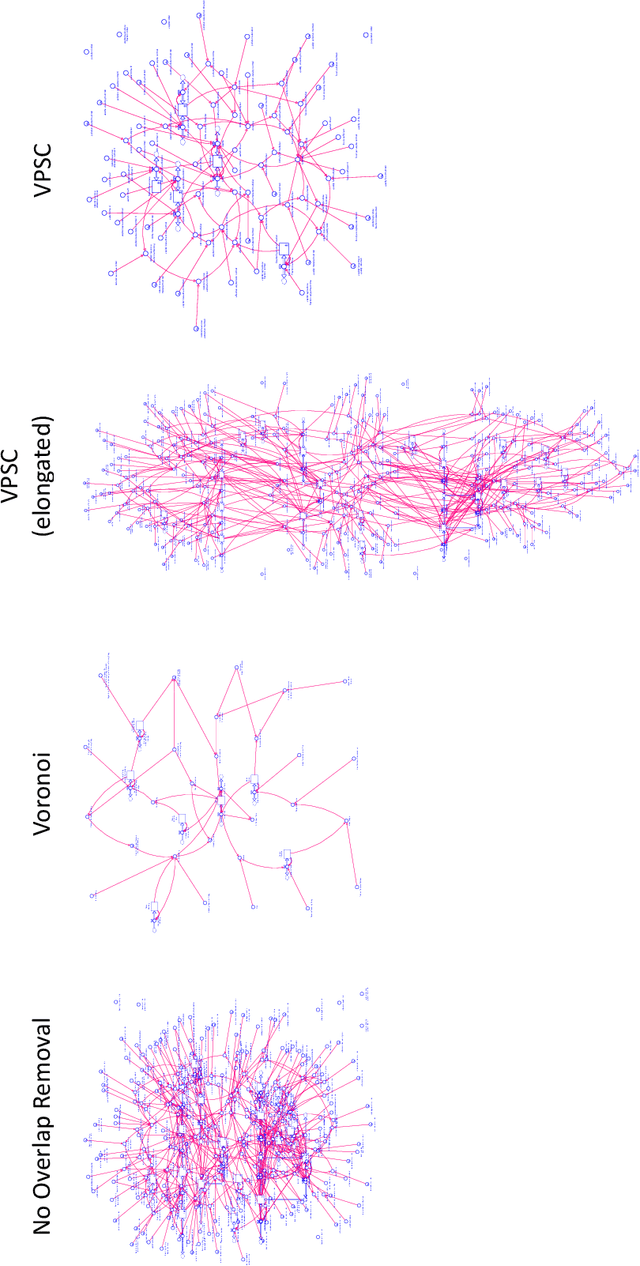
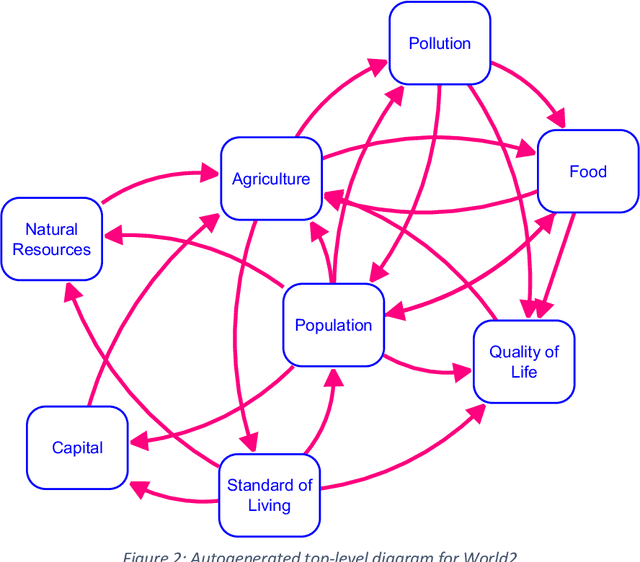
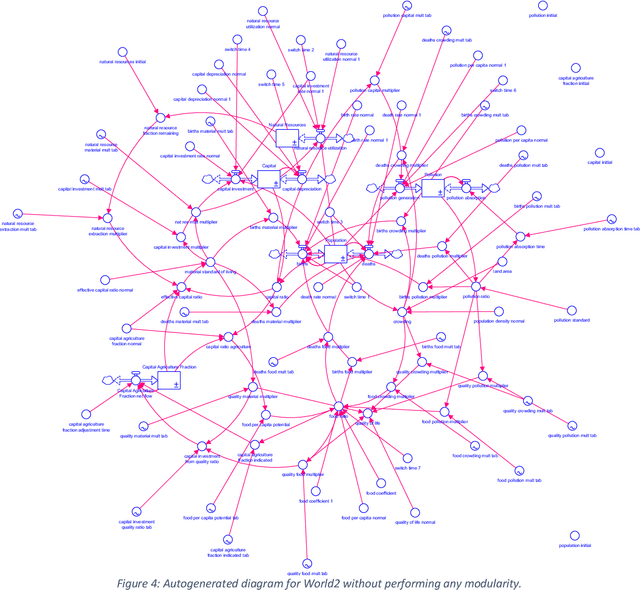
Causal loop and stock and flow diagrams are broadly used in System Dynamics because they help organize relationships and convey meaning. Using the analytical work of Schoenberg (2019) to select what to include in a compressed model, this paper demonstrates how that information can be clearly presented in an automatically generated causal loop diagram. The diagrams are generated using tools developed by people working in graph theory and the generated diagrams are clear and aesthetically pleasing. This approach can also be built upon to generate stock and flow diagrams. Automated stock and flow diagram generation opens the door to representing models developed using only equations, regardless or origin, in a clear and easy to understand way. Because models can be large, the application of grouping techniques, again developed for graph theory, can help structure the resulting diagrams in the most usable form. This paper describes the algorithms developed for automated diagram generation and shows a number of examples of their uses in large models. The application of these techniques to existing, but inaccessible, equation-based models can help broaden the knowledge base for System Dynamics modeling. The techniques can also be used to improve layout in all, or part, of existing models with diagrammatic informtion.

Finding the Loops that Matter

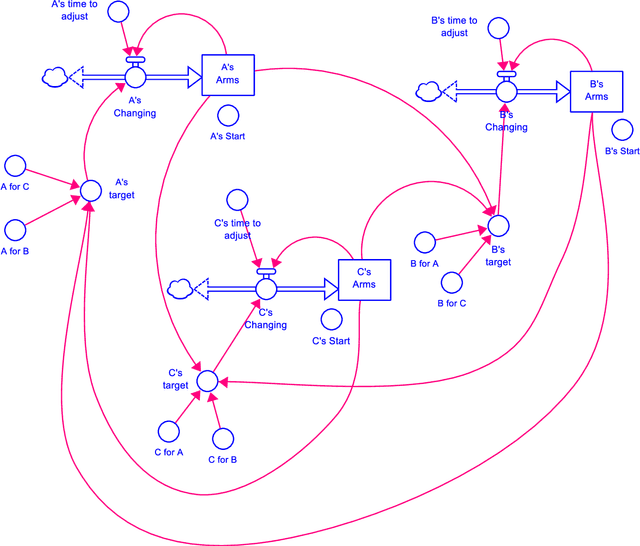
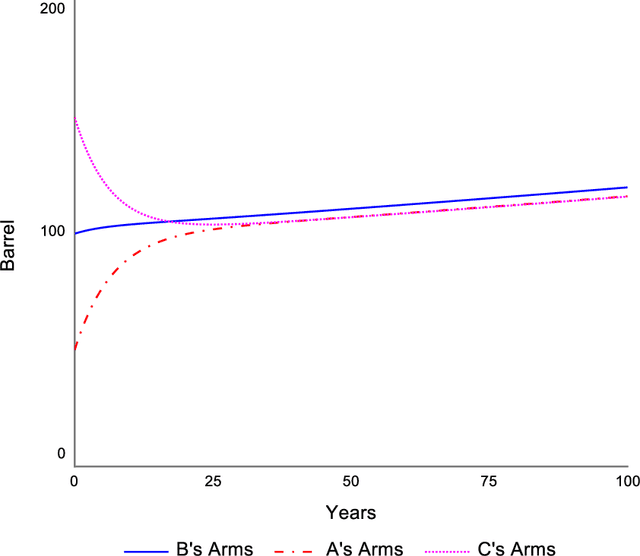
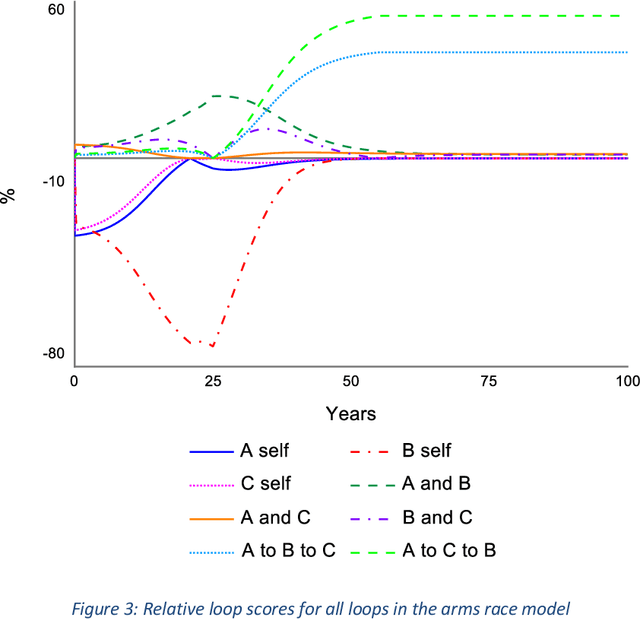
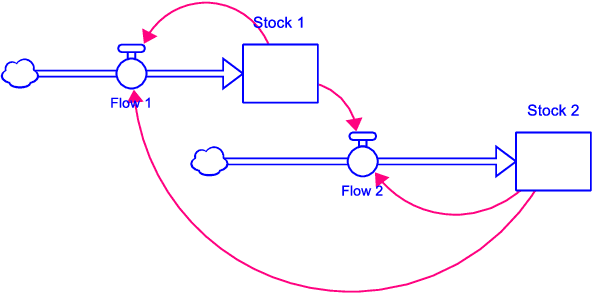
The Loops that Matter method (Schoenberg et. al, 2019) for understanding model behavior provides metrics showing the contribution of the feedback loops in a model to behavior at each point in time. To provide these metrics, it is necessary find the set of loops on which to compute them. We show in this paper the necessity of including loops that are important at different points in the simulation. These important loops may not be independent of one another and cannot be determined from static analysis of the model structure. We then describe an algorithm that can be used to discover the most important loops in models that are too feedback rich for exhaustive loop discovery. We demonstrate the use of this algorithm in terms of its ability to find the most explanatory loops, and its computational performance for large models. By using this approach, the Loops that Matter method can be applied to models of any size or complexity.

Causally interpretable multi-step time series forecasting: A new machine learning approach using simulated differential equations

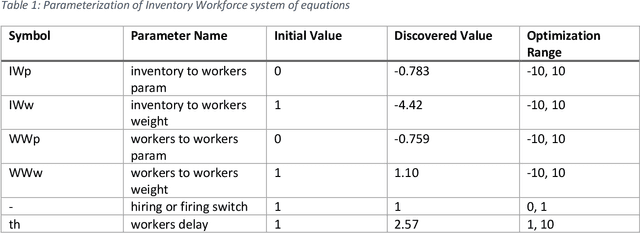
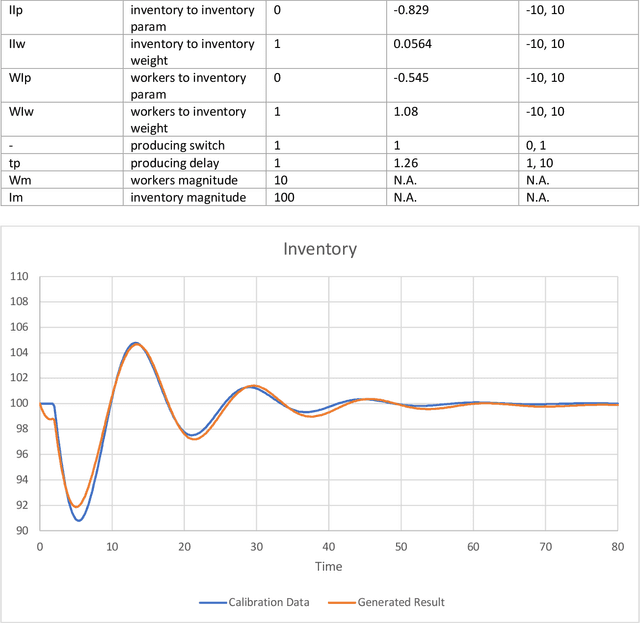
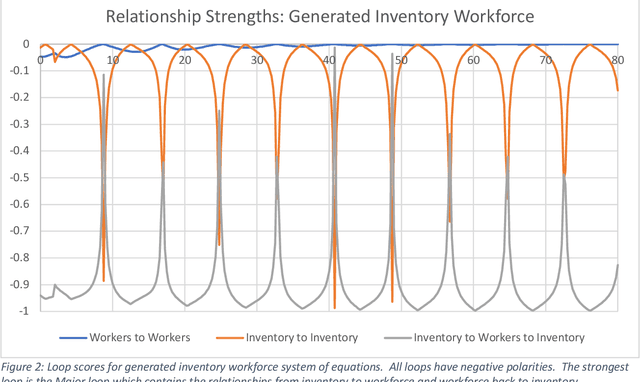
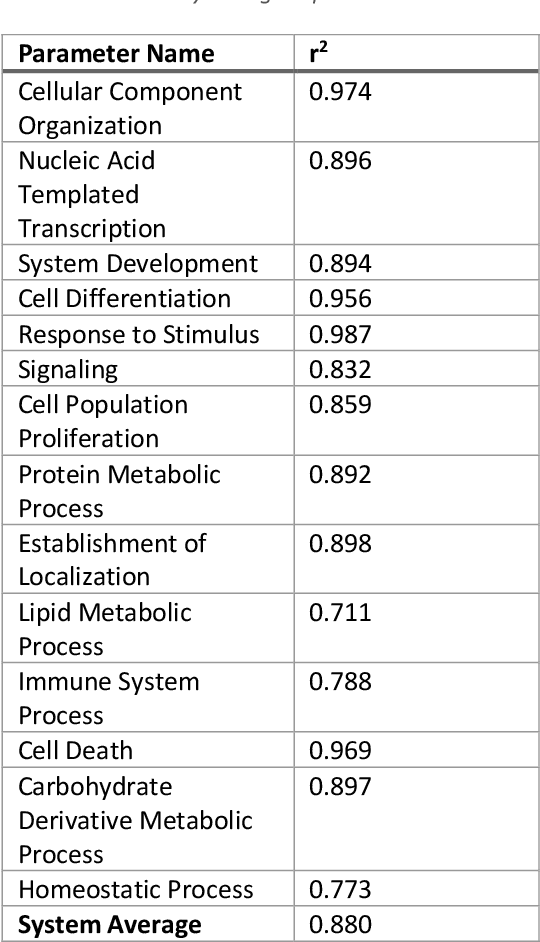
This work represents a new approach which generates then analyzes a highly non linear complex system of differential equations to do interpretable time series forecasting at a high level of accuracy. This approach provides insight and understanding into the mechanisms responsible for generating past and future behavior. Core to this method is the construction of a highly non linear complex system of differential equations that is then analyzed to determine the origins of behavior. This paper demonstrates the technique on Mass and Senge's two state Inventory Workforce model (1975) and then explores its application to the real world problem of organogenesis in mice. The organogenesis application consists of a fourteen state system where the generated set of equations reproduces observed behavior with a high level of accuracy (0.880 r^2) and when analyzed produces an interpretable and causally plausible explanation for the observed behavior.