Fast Likelihood-Free Parameter Estimation for Lévy Processes

L\'evy processes are widely used in financial modeling due to their ability to capture discontinuities and heavy tails, which are common in high-frequency asset return data. However, parameter estimation remains a challenge when associated likelihoods are unavailable or costly to compute. We propose a fast and accurate method for L\'evy parameter estimation using the neural Bayes estimation (NBE) framework -- a simulation-based, likelihood-free approach that leverages permutation-invariant neural networks to approximate Bayes estimators. Through extensive simulations across several L\'evy models, we show that NBE outperforms traditional methods in both accuracy and runtime, while also enabling rapid bootstrap-based uncertainty quantification. We illustrate our approach on a challenging high-frequency cryptocurrency return dataset, where the method captures evolving parameter dynamics and delivers reliable and interpretable inference at a fraction of the computational cost of traditional methods. NBE provides a scalable and practical solution for inference in complex financial models, enabling parameter estimation and uncertainty quantification over an entire year of data in just seconds. We additionally investigate nearly a decade of high-frequency Bitcoin returns, requiring less than one minute to estimate parameters under the proposed approach.

Modeling massive multivariate spatial data with the basis graphical lasso

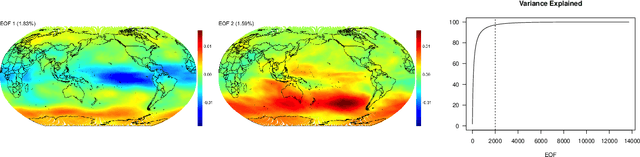
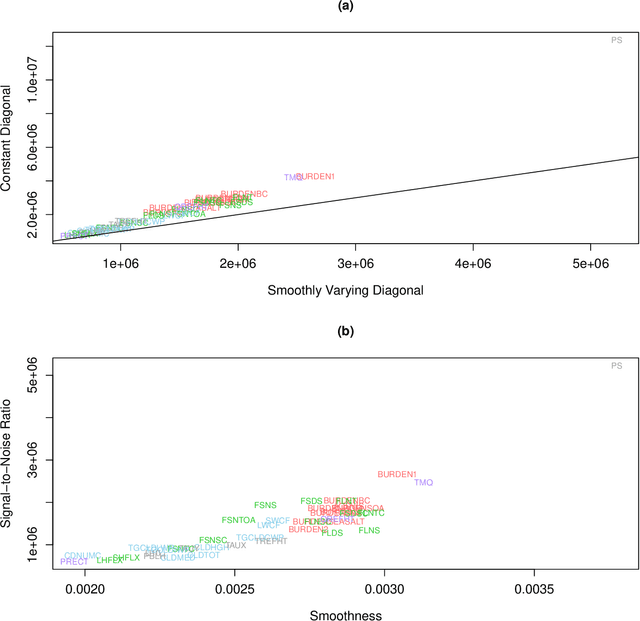
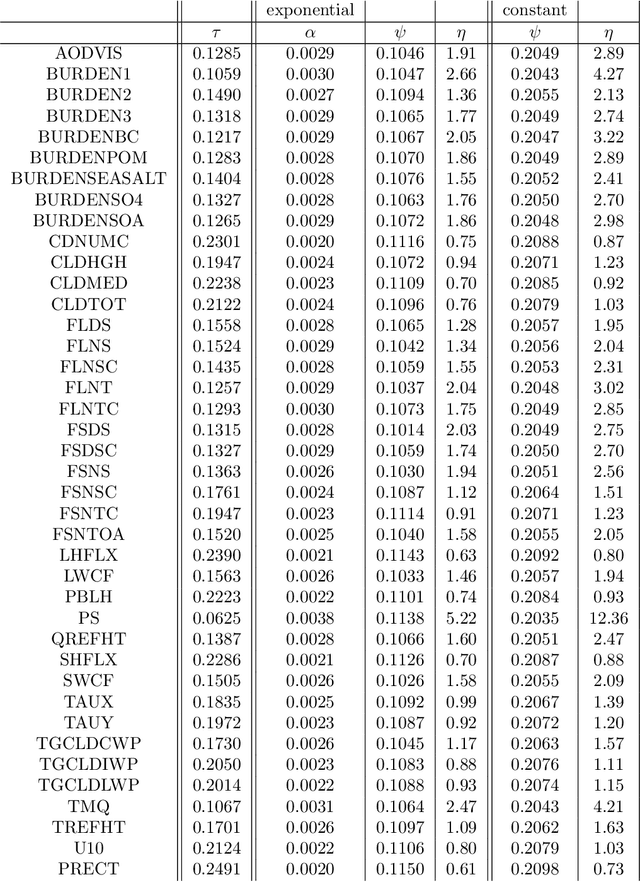
We propose a new modeling framework for highly multivariate spatial processes that synthesizes ideas from recent multiscale and spectral approaches with graphical models. The basis graphical lasso writes a univariate Gaussian process as a linear combination of basis functions weighted with entries of a Gaussian graphical vector whose graph is estimated from optimizing an $\ell_1$ penalized likelihood. This paper extends the setting to a multivariate Gaussian process where the basis functions are weighted with Gaussian graphical vectors. We motivate a model where the basis functions represent different levels of resolution and the graphical vectors for each level are assumed to be independent. Using an orthogonal basis grants linear complexity and memory usage in the number of spatial locations, the number of basis functions, and the number of realizations. An additional fusion penalty encourages a parsimonious conditional independence structure in the multilevel graphical model. We illustrate our method on a large climate ensemble from the National Center for Atmospheric Research's Community Atmosphere Model that involves 40 spatial processes.