Machine learning moment closure models for the radiative transfer equation II: enforcing global hyperbolicity in gradient based closures

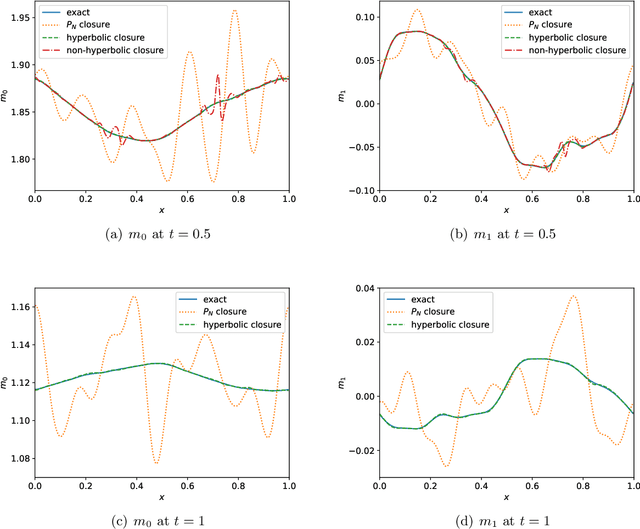
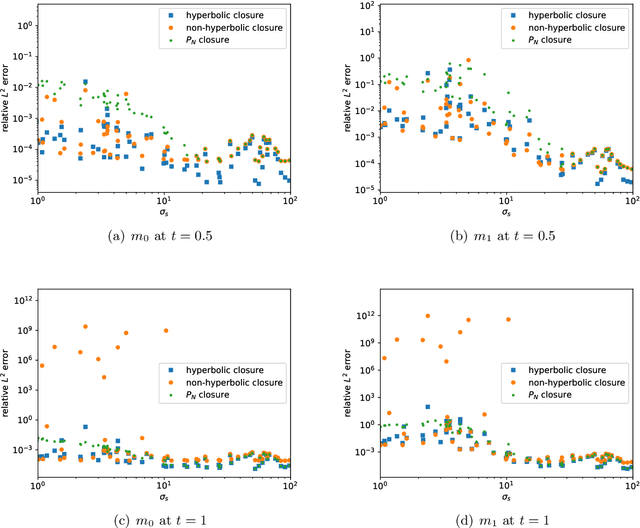
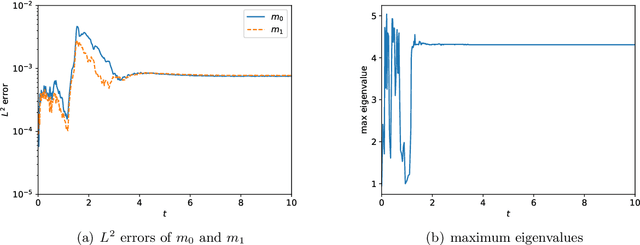
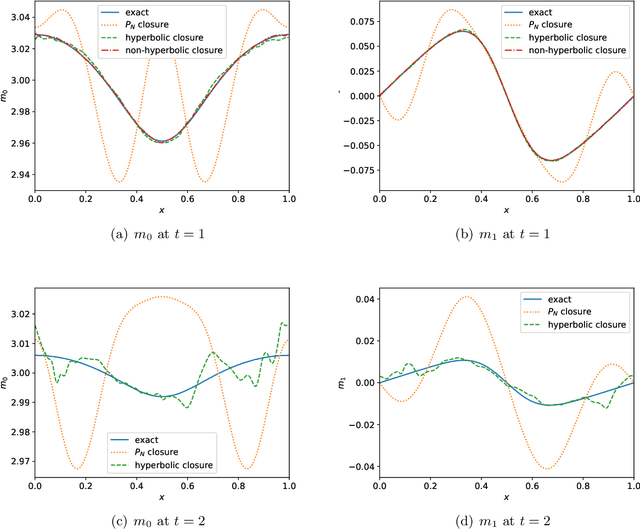
This is the second paper in a series in which we develop machine learning (ML) moment closure models for the radiative transfer equation (RTE). In our previous work \cite{huang2021gradient}, we proposed an approach to directly learn the gradient of the unclosed high order moment, which performs much better than learning the moment itself and the conventional $P_N$ closure. However, the ML moment closure model in \cite{huang2021gradient} is not able to guarantee hyperbolicity and long time stability. We propose in this paper a method to enforce the global hyperbolicity of the ML closure model. The main idea is to seek a symmetrizer (a symmetric positive definite matrix) for the closure system, and derive constraints such that the system is globally symmetrizable hyperbolic. It is shown that the new ML closure system inherits the dissipativeness of the RTE and preserves the correct diffusion limit as the Knunsden number goes to zero. Several benchmark tests including the Gaussian source problem and the two-material problem show the good accuracy, long time stability and generalizability of our globally hyperbolic ML closure model.

Data-driven discovery of multiscale chemical reactions governed by the law of mass action

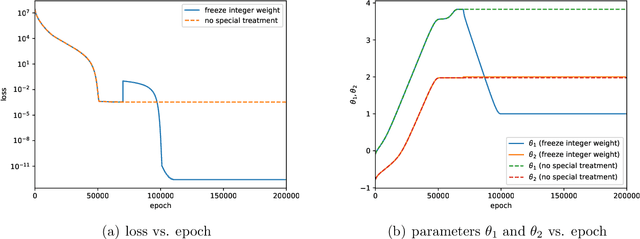
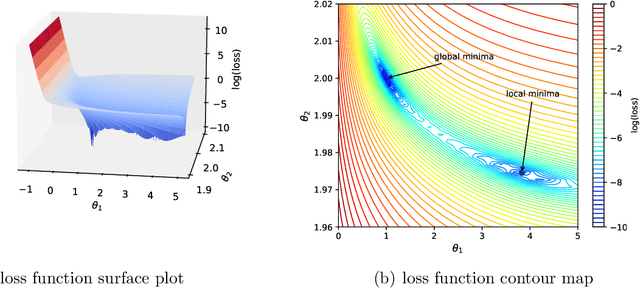
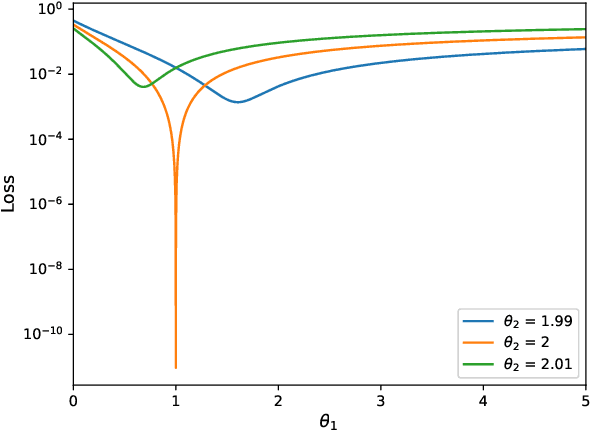
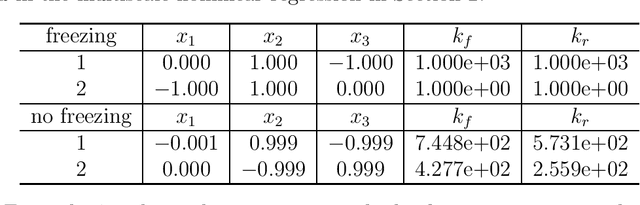
In this paper, we propose a data-driven method to discover multiscale chemical reactions governed by the law of mass action. First, we use a single matrix to represent the stoichiometric coefficients for both the reactants and products in a system without catalysis reactions. The negative entries in the matrix denote the stoichiometric coefficients for the reactants and the positive ones for the products. Second, we find that the conventional optimization methods usually get stuck in the local minima and could not find the true solution in learning the multiscale chemical reactions. To overcome this difficulty, we propose a partial-parameters-freezing (PPF) technique to progressively determine the network parameters by using the fact that the stoichiometric coefficients are integers. With such a technique, the dimension of the searching space is gradually reduced in the training process and the global mimina can be eventually obtained. Several numerical experiments including the classical Michaelis-Menten kinetics and the hydrogen oxidation reactions verify the good performance of our algorithm in learning the multiscale chemical reactions. The code is available at \url{https://github.com/JuntaoHuang/multiscale-chemical-reaction}.

Learning Interpretable and Thermodynamically Stable Partial Differential Equations

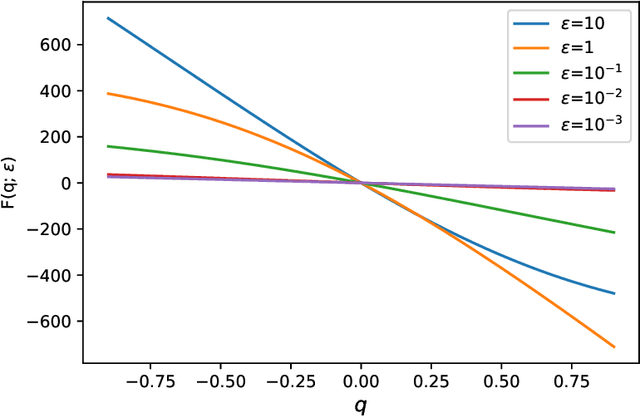
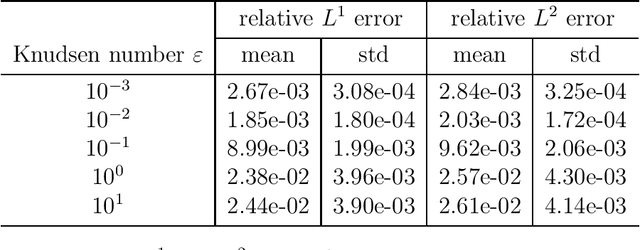
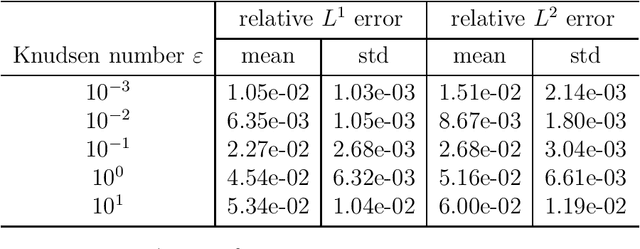
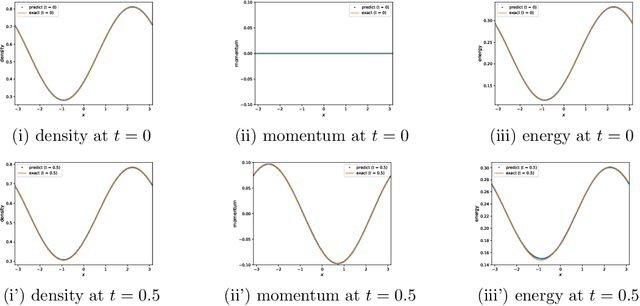
In this work, we develop a method for learning interpretable and thermodynamically stable partial differential equations (PDEs) based on the Conservation-dissipation Formalism of irreversible thermodynamics. As governing equations for non-equilibrium flows in one dimension, the learned PDEs are parameterized by fully-connected neural networks and satisfy the conservation-dissipation principle automatically. In particular, they are hyperbolic balance laws. The training data are generated from a kinetic model with smooth initial data. Numerical results indicate that the learned PDEs can achieve good accuracy in a wide range of Knudsen numbers. Remarkably, the learned dynamics can give satisfactory results with randomly sampled discontinuous initial data although it is trained only with smooth initial data.