On confidence intervals for precision matrices and the eigendecomposition of covariance matrices

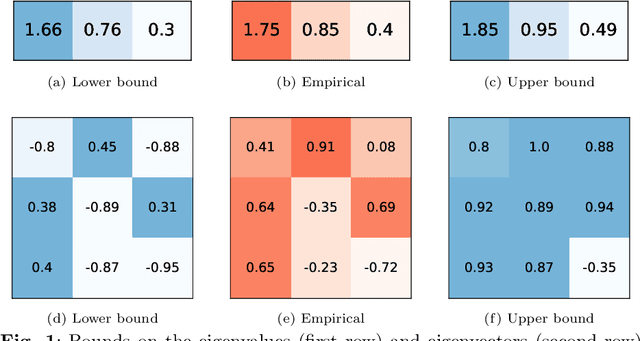
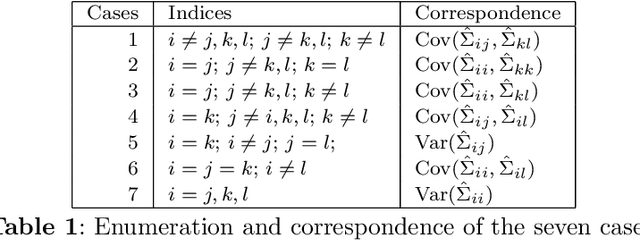
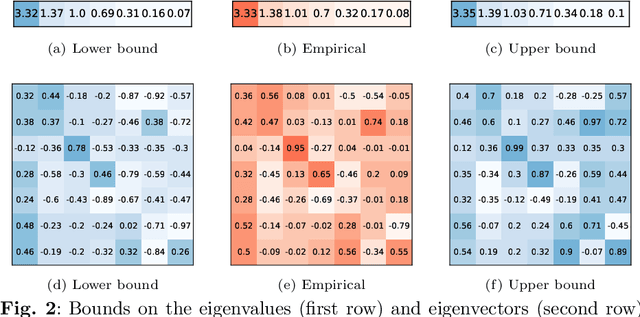
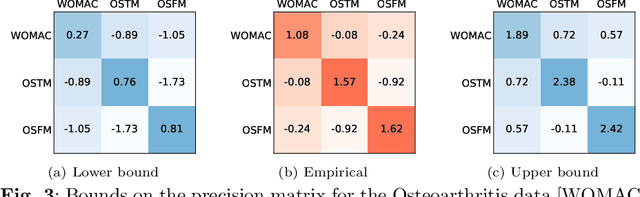
The eigendecomposition of a matrix is the central procedure in probabilistic models based on matrix factorization, for instance principal component analysis and topic models. Quantifying the uncertainty of such a decomposition based on a finite sample estimate is essential to reasoning under uncertainty when employing such models. This paper tackles the challenge of computing confidence bounds on the individual entries of eigenvectors of a covariance matrix of fixed dimension. Moreover, we derive a method to bound the entries of the inverse covariance matrix, the so-called precision matrix. The assumptions behind our method are minimal and require that the covariance matrix exists, and its empirical estimator converges to the true covariance. We make use of the theory of U-statistics to bound the $L_2$ perturbation of the empirical covariance matrix. From this result, we obtain bounds on the eigenvectors using Weyl's theorem and the eigenvalue-eigenvector identity and we derive confidence intervals on the entries of the precision matrix using matrix inversion perturbation bounds. As an application of these results, we demonstrate a new statistical test, which allows us to test for non-zero values of the precision matrix. We compare this test to the well-known Fisher-z test for partial correlations, and demonstrate the soundness and scalability of the proposed statistical test, as well as its application to real-world data from medical and physics domains.

Fast Non-Parametric Tests of Relative Dependency and Similarity

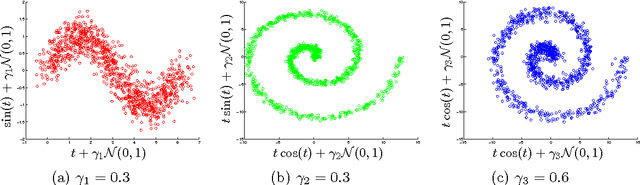
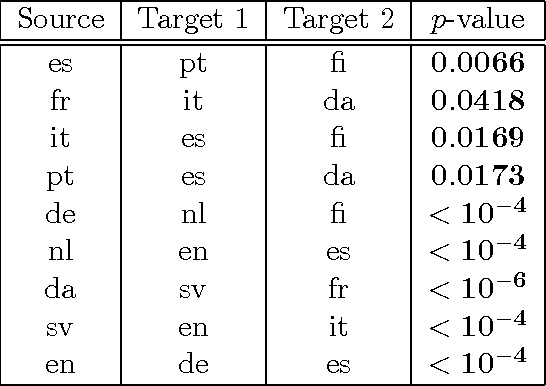
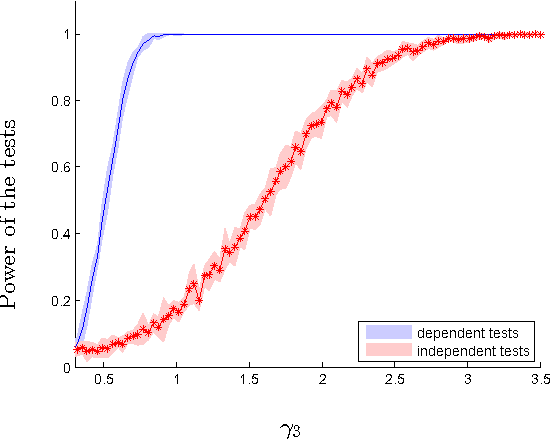
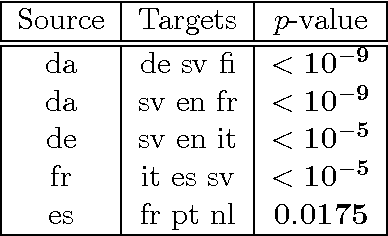
We introduce two novel non-parametric statistical hypothesis tests. The first test, called the relative test of dependency, enables us to determine whether one source variable is significantly more dependent on a first target variable or a second. Dependence is measured via the Hilbert-Schmidt Independence Criterion (HSIC). The second test, called the relative test of similarity, is use to determine which of the two samples from arbitrary distributions is significantly closer to a reference sample of interest and the relative measure of similarity is based on the Maximum Mean Discrepancy (MMD). To construct these tests, we have used as our test statistics the difference of HSIC statistics and of MMD statistics, respectively. The resulting tests are consistent and unbiased, and have favorable convergence properties. The effectiveness of the relative dependency test is demonstrated on several real-world problems: we identify languages groups from a multilingual parallel corpus, and we show that tumor location is more dependent on gene expression than chromosome imbalance. We also demonstrate the performance of the relative test of similarity over a broad selection of model comparisons problems in deep generative models.

A U-statistic Approach to Hypothesis Testing for Structure Discovery in Undirected Graphical Models

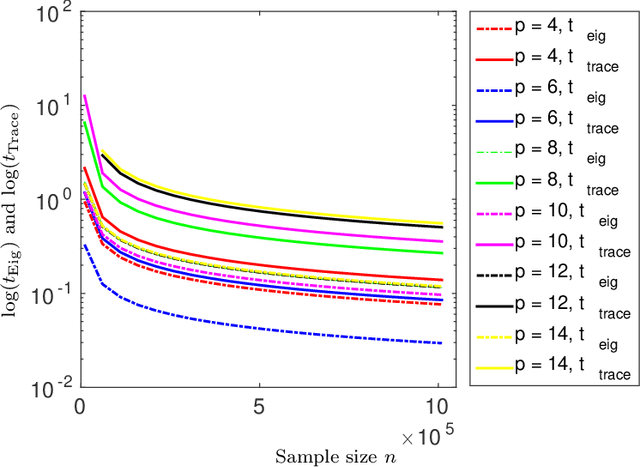
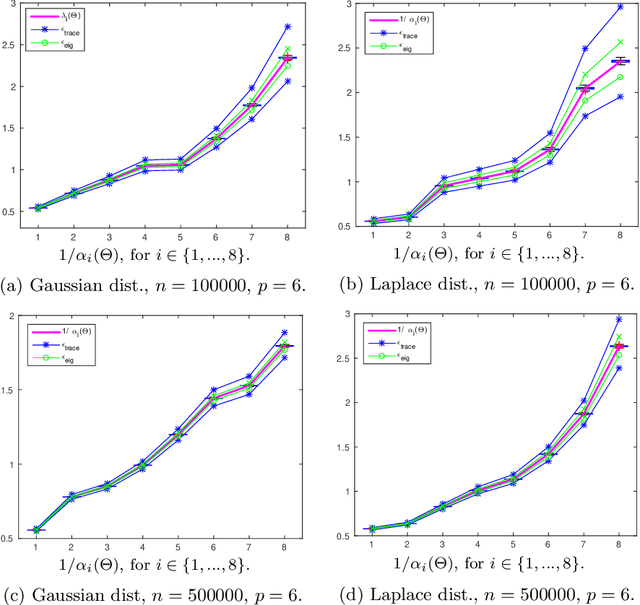
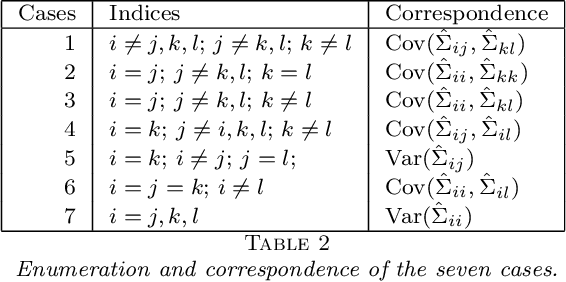
Structure discovery in graphical models is the determination of the topology of a graph that encodes conditional independence properties of the joint distribution of all variables in the model. For some class of probability distributions, an edge between two variables is present if and only if the corresponding entry in the precision matrix is non-zero. For a finite sample estimate of the precision matrix, entries close to zero may be due to low sample effects, or due to an actual association between variables; these two cases are not readily distinguishable. %Fisher provided a hypothesis test based on a parametric approximation to the distribution of an entry in the precision matrix of a Gaussian distribution, but this may not provide valid upper bounds on $p$-values for non-Gaussian distributions. Many related works on this topic consider potentially restrictive distributional or sparsity assumptions that may not apply to a data sample of interest, and direct estimation of the uncertainty of an estimate of the precision matrix for general distributions remains challenging. Consequently, we make use of results for $U$-statistics and apply them to the covariance matrix. By probabilistically bounding the distortion of the covariance matrix, we can apply Weyl's theorem to bound the distortion of the precision matrix, yielding a conservative, but sound test threshold for a much wider class of distributions than considered in previous works. The resulting test enables one to answer with statistical significance whether an edge is present in the graph, and convergence results are known for a wide range of distributions. The computational complexities is linear in the sample size enabling the application of the test to large data samples for which computation time becomes a limiting factor. We experimentally validate the correctness and scalability of the test on multivariate distributions for which the distributional assumptions of competing tests result in underestimates of the false positive ratio. By contrast, the proposed test remains sound, promising to be a useful tool for hypothesis testing for diverse real-world problems.

A Test of Relative Similarity For Model Selection in Generative Models

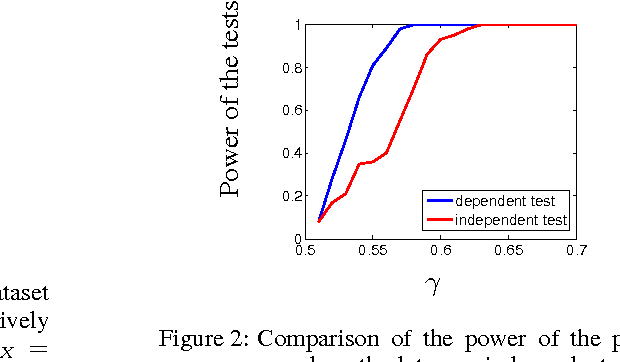
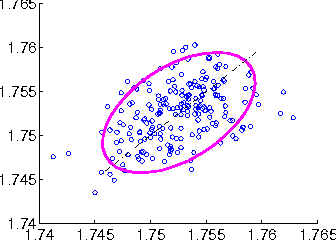
Probabilistic generative models provide a powerful framework for representing data that avoids the expense of manual annotation typically needed by discriminative approaches. Model selection in this generative setting can be challenging, however, particularly when likelihoods are not easily accessible. To address this issue, we introduce a statistical test of relative similarity, which is used to determine which of two models generates samples that are significantly closer to a real-world reference dataset of interest. We use as our test statistic the difference in maximum mean discrepancies (MMDs) between the reference dataset and each model dataset, and derive a powerful, low-variance test based on the joint asymptotic distribution of the MMDs between each reference-model pair. In experiments on deep generative models, including the variational auto-encoder and generative moment matching network, the tests provide a meaningful ranking of model performance as a function of parameter and training settings.

A low variance consistent test of relative dependency

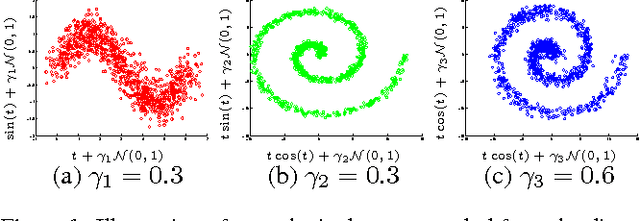
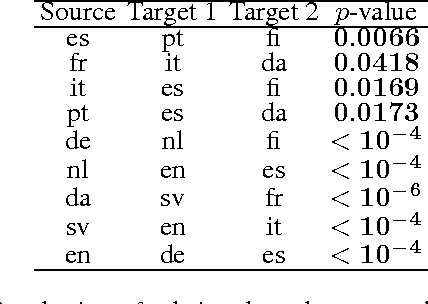
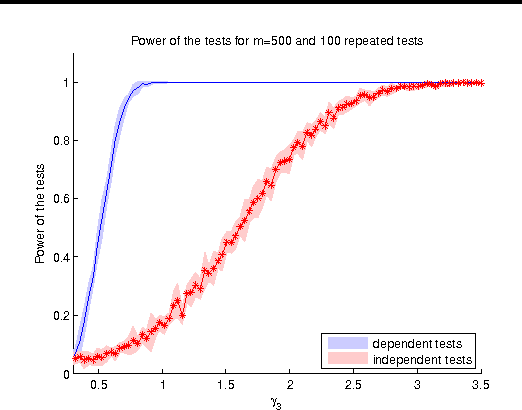
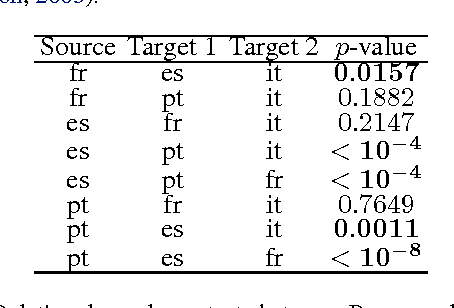
We describe a novel non-parametric statistical hypothesis test of relative dependence between a source variable and two candidate target variables. Such a test enables us to determine whether one source variable is significantly more dependent on a first target variable or a second. Dependence is measured via the Hilbert-Schmidt Independence Criterion (HSIC), resulting in a pair of empirical dependence measures (source-target 1, source-target 2). We test whether the first dependence measure is significantly larger than the second. Modeling the covariance between these HSIC statistics leads to a provably more powerful test than the construction of independent HSIC statistics by sub-sampling. The resulting test is consistent and unbiased, and (being based on U-statistics) has favorable convergence properties. The test can be computed in quadratic time, matching the computational complexity of standard empirical HSIC estimators. The effectiveness of the test is demonstrated on several real-world problems: we identify language groups from a multilingual corpus, and we prove that tumor location is more dependent on gene expression than chromosomal imbalances. Source code is available for download at https://github.com/wbounliphone/reldep.