Semidefinite Programming for Quantum Channel Learning

The problem of reconstructing a quantum channel from a sample of classical data is considered. When the total fidelity can be represented as a ratio of two quadratic forms (e.g., in the case of mapping a mixed state to a pure state, projective operators, unitary learning, and others), Semidefinite Programming (SDP) can be applied to solve the fidelity optimization problem with respect to the Choi matrix. A remarkable feature of SDP is that the optimization is convex, which allows the problem to be efficiently solved by a variety of numerical algorithms. We have tested several commercially available SDP solvers, all of which allowed for the reconstruction of quantum channels of different forms. A notable feature is that the Kraus rank of the obtained quantum channel typically comprises less than a few percent of its maximal possible value. This suggests that a relatively small Kraus rank quantum channel is typically sufficient to describe experimentally observed classical data. The theory was also applied to the problem of reconstructing projective operators from data. Finally, we discuss a classical computational model based on quantum channel transformation, performed and calculated on a classical computer, possibly hardware-optimized.

On Quantum Channel Learning

The problem of an optimal mapping between Hilbert spaces $IN$ and $OUT$, based on a series of density matrix mapping measurements $\rho^{(l)} \to \varrho^{(l)}$, $l=1\dots M$, is formulated as an optimization problem maximizing the total fidelity $\mathcal{F}=\sum_{l=1}^{M} \omega^{(l)} F\left(\varrho^{(l)},\sum_s B_s \rho^{(l)} B^{\dagger}_s\right)$ subject to probability preservation constraints on Kraus operators $B_s$. For $F(\varrho,\sigma)$ in the form that total fidelity can be represented as a quadratic form with superoperator $\mathcal{F}=\sum_s\left\langle B_s\middle|S\middle| B_s \right\rangle$ (either exactly or as an approximation) an iterative algorithm is developed to find the global maximum. The result comprises in $N_s$ operators $B_s$ that collectively form an $IN$ to $OUT$ quantum channel $A^{OUT}=\sum_s B_s A^{IN} B_s^{\dagger}$. The work introduces two important generalizations of unitary learning: 1. $IN$/$OUT$ states are represented as density matrices. 2. The mapping itself is formulated as a general quantum channel. This marks a crucial advancement from the commonly studied unitary mapping of pure states $\phi_l=\mathcal{U} \psi_l$ to a general quantum channel, what allows us to distinguish probabilistic mixture of states and their superposition. An application of the approach is demonstrated on unitary learning of density matrix mapping $\varrho^{(l)}=\mathcal{U} \rho^{(l)} \mathcal{U}^{\dagger}$, in this case a quadratic on $\mathcal{U}$ fidelity can be constructed by considering $\sqrt{\rho^{(l)}} \to \sqrt{\varrho^{(l)}}$ mapping, and on a general quantum channel of Kraus rank $N_s$, where quadratic on $B_s$ fidelity is an approximation -- a quantum channel is then built as a hierarchy of unitary mappings. The approach can be applied to study decoherence effects, spontaneous coherence, synchronizing, etc.

On Partially Unitary Learning

The problem of an optimal mapping between Hilbert spaces $IN$ of $\left|\psi\right\rangle$ and $OUT$ of $\left|\phi\right\rangle$ based on a set of wavefunction measurements (within a phase) $\psi_l \to \phi_l$, $l=1\dots M$, is formulated as an optimization problem maximizing the total fidelity $\sum_{l=1}^{M} \omega^{(l)} \left|\langle\phi_l|\mathcal{U}|\psi_l\rangle\right|^2$ subject to probability preservation constraints on $\mathcal{U}$ (partial unitarity). Constructed operator $\mathcal{U}$ can be considered as a $IN$ to $OUT$ quantum channel; it is a partially unitary rectangular matrix of the dimension $\dim(OUT) \times \dim(IN)$ transforming operators as $A^{OUT}=\mathcal{U} A^{IN} \mathcal{U}^{\dagger}$. An iteration algorithm finding the global maximum of this optimization problem is developed and it's application to a number of problems is demonstrated. A software product implementing the algorithm is available from the authors.

On Machine Learning Knowledge Representation In The Form Of Partially Unitary Operator. Knowledge Generalizing Operator

A new form of ML knowledge representation with high generalization power is developed and implemented numerically. Initial $\mathit{IN}$ attributes and $\mathit{OUT}$ class label are transformed into the corresponding Hilbert spaces by considering localized wavefunctions. A partially unitary operator optimally converting a state from $\mathit{IN}$ Hilbert space into $\mathit{OUT}$ Hilbert space is then built from an optimization problem of transferring maximal possible probability from $\mathit{IN}$ to $\mathit{OUT}$, this leads to the formulation of a new algebraic problem. Constructed Knowledge Generalizing Operator $\mathcal{U}$ can be considered as a $\mathit{IN}$ to $\mathit{OUT}$ quantum channel; it is a partially unitary rectangular matrix of the dimension $\mathrm{dim}(\mathit{OUT}) \times \mathrm{dim}(\mathit{IN})$ transforming operators as $A^{\mathit{OUT}}=\mathcal{U} A^{\mathit{IN}} \mathcal{U}^{\dagger}$. Whereas only operator $\mathcal{U}$ projections squared are observable $\left\langle\mathit{OUT}|\mathcal{U}|\mathit{IN}\right\rangle^2$ (probabilities), the fundamental equation is formulated for the operator $\mathcal{U}$ itself. This is the reason of high generalizing power of the approach; the situation is the same as for the Schr\"{o}dinger equation: we can only measure $\psi^2$, but the equation is written for $\psi$ itself.

On The Radon--Nikodym Spectral Approach With Optimal Clustering

Problems of interpolation, classification, and clustering are considered. In the tenets of Radon--Nikodym approach $\langle f(\mathbf{x})\psi^2 \rangle / \langle\psi^2\rangle$, where the $\psi(\mathbf{x})$ is a linear function on input attributes, all the answers are obtained from a generalized eigenproblem $|f|\psi^{[i]}\rangle = \lambda^{[i]} |\psi^{[i]}\rangle$. The solution to the interpolation problem is a regular Radon-Nikodym derivative. The solution to the classification problem requires prior and posterior probabilities that are obtained using the Lebesgue quadrature[1] technique. Whereas in a Bayesian approach new observations change only outcome probabilities, in the Radon-Nikodym approach not only outcome probabilities but also the probability space $|\psi^{[i]}\rangle$ change with new observations. This is a remarkable feature of the approach: both the probabilities and the probability space are constructed from the data. The Lebesgue quadrature technique can be also applied to the optimal clustering problem. The problem is solved by constructing a Gaussian quadrature on the Lebesgue measure. A distinguishing feature of the Radon-Nikodym approach is the knowledge of the invariant group: all the answers are invariant relatively any non-degenerated linear transform of input vector $\mathbf{x}$ components. A software product implementing the algorithms of interpolation, classification, and optimal clustering is available from the authors.

On Lebesgue Integral Quadrature

A new type of quadrature is developed. The Gauss quadrature, for a given measure, finds optimal values of a function's argument (nodes) and the corresponding weights. In contrast, the Lebesgue quadrature developed in this paper, finds optimal values of function (value-nodes) and the corresponding weights. The Gauss quadrature groups sums by function argument, it can be viewed as a $n$-point discrete measure, producing the Riemann integral. The Lebesgue quadrature groups sums by function value, it can be viewed as a $n$-point discrete distribution, producing the Lebesgue integral. Mathematically, the problem is reduced to a generalized eigenvalue problem: Lebesgue quadrature value-nodes are the eigenvalues and the corresponding weights are the square of the averaged eigenvectors. A numerical estimation of an integral as the Lebesgue integral is especially advantageous when analyzing irregular and stochastic processes. The approach separates the outcome (value-nodes) and the probability of the outcome (weight). For this reason, it is especially well-suited for the study of non--Gaussian processes. The software implementing the theory is available from the authors.

On Numerical Estimation of Joint Probability Distribution from Lebesgue Integral Quadratures

An important application of Lebesgue integral quadrature[1] is developed. Given two random processes, $f(x)$ and $g(x)$, two generalized eigenvalue problems can be formulated and solved. In addition to obtaining two Lebesgue quadratures (for $f$ and $g$) from two eigenproblems, the projections of $f$-- and $g$-- eigenvectors on each other allow to build a joint distribution estimator, the most general form of which is a density--matrix correlation. The examples of the density--matrix correlation can be the value--correlation $V_{f_i;g_j}$, similar to the regular correlation concept, and a new one, the probability--correlation $P_{f_i;g_j}$. The theory is implemented numerically; the software is available under the GPLv3 license.

Radon-Nikodym approximation in application to image analysis

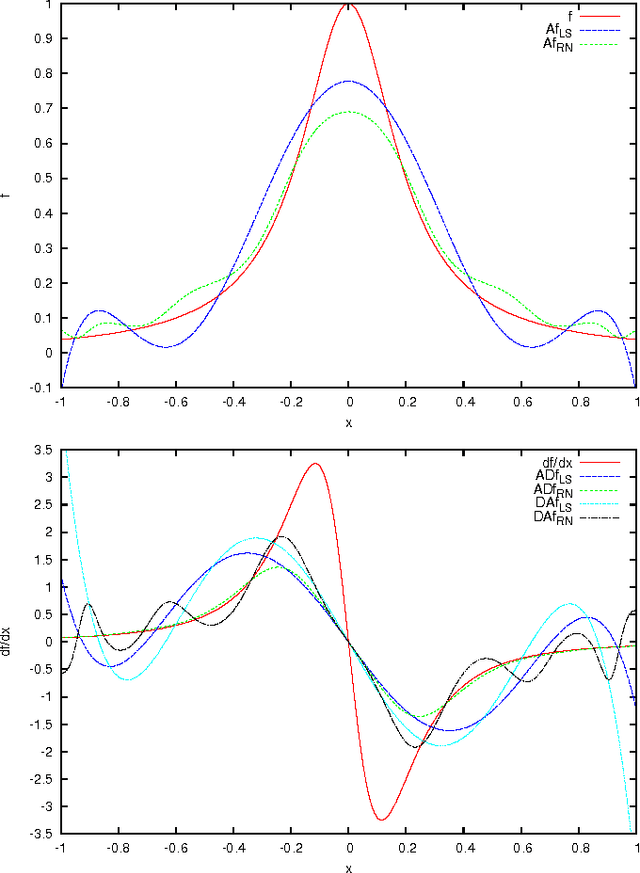
For an image pixel information can be converted to the moments of some basis $Q_k$, e.g. Fourier-Mellin, Zernike, monomials, etc. Given sufficient number of moments pixel information can be completely recovered, for insufficient number of moments only partial information can be recovered and the image reconstruction is, at best, of interpolatory type. Standard approach is to present interpolated value as a linear combination of basis functions, what is equivalent to least squares expansion. However, recent progress in numerical stability of moments estimation allows image information to be recovered from moments in a completely different manner, applying Radon-Nikodym type of expansion, what gives the result as a ratio of two quadratic forms of basis functions. In contrast with least squares the Radon-Nikodym approach has oscillation near the boundaries very much suppressed and does not diverge outside of basis support. While least squares theory operate with vectors $<fQ_k>$, Radon-Nikodym theory operates with matrices $<fQ_jQ_k>$, what make the approach much more suitable to image transforms and statistical property estimation.

Norm-Free Radon-Nikodym Approach to Machine Learning

For Machine Learning (ML) classification problem, where a vector of $\mathbf{x}$--observations (values of attributes) is mapped to a single $y$ value (class label), a generalized Radon--Nikodym type of solution is proposed. Quantum--mechanics --like probability states $\psi^2(\mathbf{x})$ are considered and "Cluster Centers", corresponding to the extremums of $<y\psi^2(\mathbf{x})>/<\psi^2(\mathbf{x})>$, are found from generalized eigenvalues problem. The eigenvalues give possible $y^{[i]}$ outcomes and corresponding to them eigenvectors $\psi^{[i]}(\mathbf{x})$ define "Cluster Centers". The projection of a $\psi$ state, localized at given $\mathbf{x}$ to classify, on these eigenvectors define the probability of $y^{[i]}$ outcome, thus avoiding using a norm ($L^2$ or other types), required for "quality criteria" in a typical Machine Learning technique. A coverage of each `Cluster Center" is calculated, what potentially allows to separate system properties (described by $y^{[i]}$ outcomes) and system testing conditions (described by $C^{[i]}$ coverage). As an example of such application $y$ distribution estimator is proposed in a form of pairs $(y^{[i]},C^{[i]})$, that can be considered as Gauss quadratures generalization. This estimator allows to perform $y$ probability distribution estimation in a strongly non--Gaussian case.

Multiple-Instance Learning: Radon-Nikodym Approach to Distribution Regression Problem

For distribution regression problem, where a bag of $x$--observations is mapped to a single $y$ value, a one--step solution is proposed. The problem of random distribution to random value is transformed to random vector to random value by taking distribution moments of $x$ observations in a bag as random vector. Then Radon--Nikodym or least squares theory can be applied, what give $y(x)$ estimator. The probability distribution of $y$ is also obtained, what requires solving generalized eigenvalues problem, matrix spectrum (not depending on $x$) give possible $y$ outcomes and depending on $x$ probabilities of outcomes can be obtained by projecting the distribution with fixed $x$ value (delta--function) to corresponding eigenvector. A library providing numerically stable polynomial basis for these calculations is available, what make the proposed approach practical.