Vitalii Emelianov
On the Impact of Output Perturbation on Fairness in Binary Linear Classification
Feb 05, 2024Abstract:We theoretically study how differential privacy interacts with both individual and group fairness in binary linear classification. More precisely, we focus on the output perturbation mechanism, a classic approach in privacy-preserving machine learning. We derive high-probability bounds on the level of individual and group fairness that the perturbed models can achieve compared to the original model. Hence, for individual fairness, we prove that the impact of output perturbation on the level of fairness is bounded but grows with the dimension of the model. For group fairness, we show that this impact is determined by the distribution of so-called angular margins, that is signed margins of the non-private model re-scaled by the norm of each example.
On Fair Selection in the Presence of Implicit and Differential Variance
Dec 10, 2021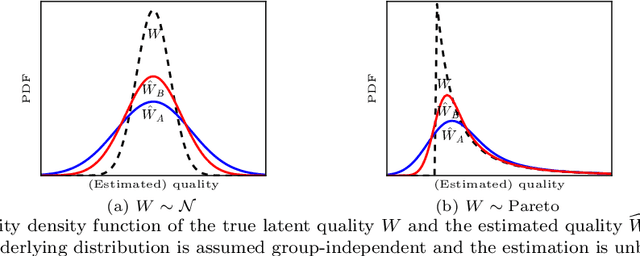

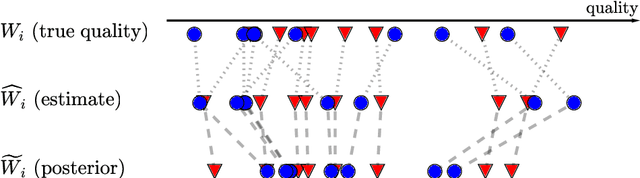
Abstract:Discrimination in selection problems such as hiring or college admission is often explained by implicit bias from the decision maker against disadvantaged demographic groups. In this paper, we consider a model where the decision maker receives a noisy estimate of each candidate's quality, whose variance depends on the candidate's group -- we argue that such differential variance is a key feature of many selection problems. We analyze two notable settings: in the first, the noise variances are unknown to the decision maker who simply picks the candidates with the highest estimated quality independently of their group; in the second, the variances are known and the decision maker picks candidates having the highest expected quality given the noisy estimate. We show that both baseline decision makers yield discrimination, although in opposite directions: the first leads to underrepresentation of the low-variance group while the second leads to underrepresentation of the high-variance group. We study the effect on the selection utility of imposing a fairness mechanism that we term the $\gamma$-rule (it is an extension of the classical four-fifths rule and it also includes demographic parity). In the first setting (with unknown variances), we prove that under mild conditions, imposing the $\gamma$-rule increases the selection utility -- here there is no trade-off between fairness and utility. In the second setting (with known variances), imposing the $\gamma$-rule decreases the utility but we prove a bound on the utility loss due to the fairness mechanism.
On Fair Selection in the Presence of Implicit Variance
Jun 24, 2020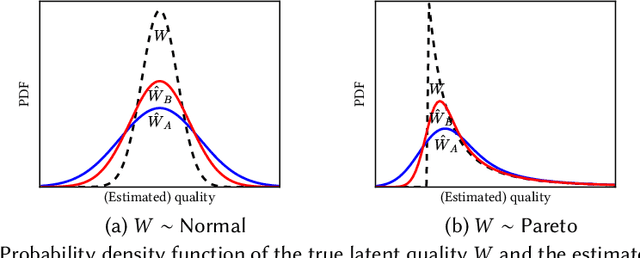

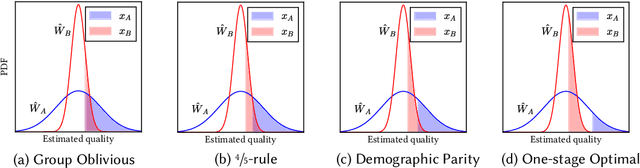
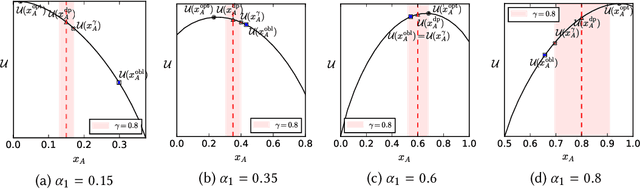
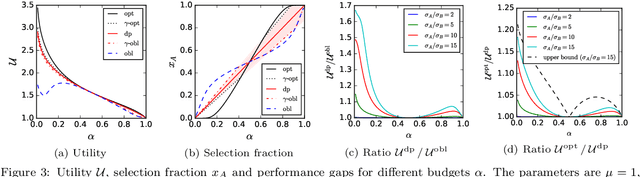
Abstract:Quota-based fairness mechanisms like the so-called Rooney rule or four-fifths rule are used in selection problems such as hiring or college admission to reduce inequalities based on sensitive demographic attributes. These mechanisms are often viewed as introducing a trade-off between selection fairness and utility. In recent work, however, Kleinberg and Raghavan showed that, in the presence of implicit bias in estimating candidates' quality, the Rooney rule can increase the utility of the selection process. We argue that even in the absence of implicit bias, the estimates of candidates' quality from different groups may differ in another fundamental way, namely, in their variance. We term this phenomenon implicit variance and we ask: can fairness mechanisms be beneficial to the utility of a selection process in the presence of implicit variance (even in the absence of implicit bias)? To answer this question, we propose a simple model in which candidates have a true latent quality that is drawn from a group-independent normal distribution. To make the selection, a decision maker receives an unbiased estimate of the quality of each candidate, with normal noise, but whose variance depends on the candidate's group. We then compare the utility obtained by imposing a fairness mechanism that we term $\gamma$-rule (it includes demographic parity and the four-fifths rule as special cases), to that of a group-oblivious selection algorithm that picks the candidates with the highest estimated quality independently of their group. Our main result shows that the demographic parity mechanism always increases the selection utility, while any $\gamma$-rule weakly increases it. We extend our model to a two-stage selection process where the true quality is observed at the second stage. We discuss multiple extensions of our results, in particular to different distributions of the true latent quality.
The Price of Local Fairness in Multistage Selection
Jun 15, 2019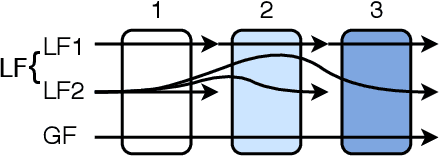
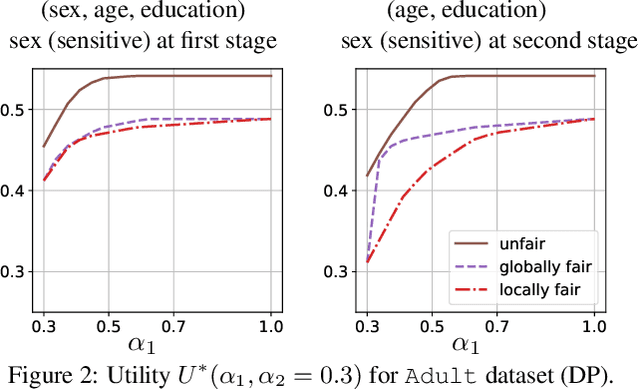
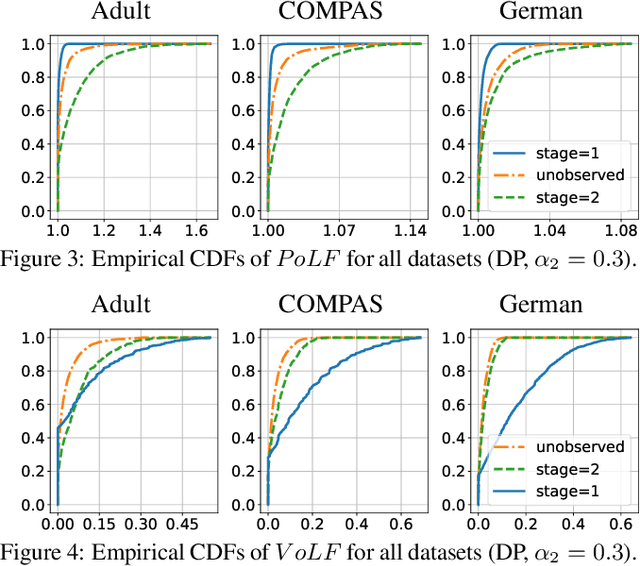
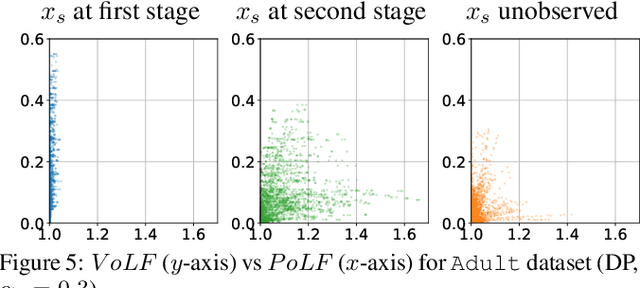
Abstract:The rise of algorithmic decision making led to active researches on how to define and guarantee fairness, mostly focusing on one-shot decision making. In several important applications such as hiring, however, decisions are made in multiple stage with additional information at each stage. In such cases, fairness issues remain poorly understood. In this paper we study fairness in $k$-stage selection problems where additional features are observed at every stage. We first introduce two fairness notions, local (per stage) and global (final stage) fairness, that extend the classical fairness notions to the $k$-stage setting. We propose a simple model based on a probabilistic formulation and show that the locally and globally fair selections that maximize precision can be computed via a linear program. We then define the price of local fairness to measure the loss of precision induced by local constraints; and investigate theoretically and empirically this quantity. In particular, our experiments show that the price of local fairness is generally smaller when the sensitive attribute is observed at the first stage; but globally fair selections are more locally fair when the sensitive attribute is observed at the second stage---hence in both cases it is often possible to have a selection that has a small price of local fairness and is close to locally fair.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge