Bayesian Joint Chance Constrained Optimization: Approximations and Statistical Consistency

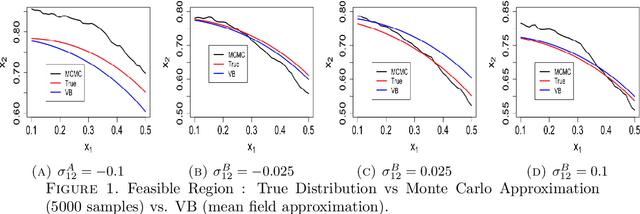
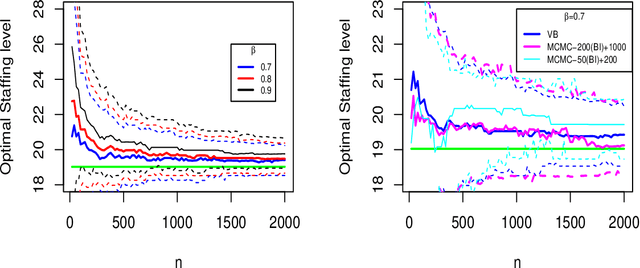
This paper considers data-driven chance-constrained stochastic optimization problems in a Bayesian framework. Bayesian posteriors afford a principled mechanism to incorporate data and prior knowledge into stochastic optimization problems. However, the computation of Bayesian posteriors is typically an intractable problem, and has spawned a large literature on approximate Bayesian computation. Here, in the context of chance-constrained optimization, we focus on the question of statistical consistency (in an appropriate sense) of the optimal value, computed using an approximate posterior distribution. To this end, we rigorously prove a frequentist consistency result demonstrating the convergence of the optimal value to the optimal value of a fixed, parameterized constrained optimization problem. We augment this by also establishing a probabilistic rate of convergence of the optimal value. We also prove the convex feasibility of the approximate Bayesian stochastic optimization problem. Finally, we demonstrate the utility of our approach on an optimal staffing problem for an M/M/c queueing model.

Variational Bayesian Methods for Stochastically Constrained System Design Problems

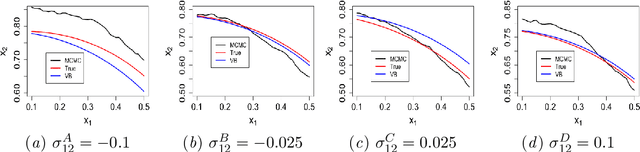
We study system design problems stated as parameterized stochastic programs with a chance-constraint set. We adopt a Bayesian approach that requires the computation of a posterior predictive integral which is usually intractable. In addition, for the problem to be a well-defined convex program, we must retain the convexity of the feasible set. Consequently, we propose a variational Bayes-based method to approximately compute the posterior predictive integral that ensures tractability and retains the convexity of the feasible set. Under certain regularity conditions, we also show that the solution set obtained using variational Bayes converges to the true solution set as the number of observations tends to infinity. We also provide bounds on the probability of qualifying a true infeasible point (with respect to the true constraints) as feasible under the VB approximation for a given number of samples.

Asymptotic Consistency of Loss-Calibrated Variational Bayes

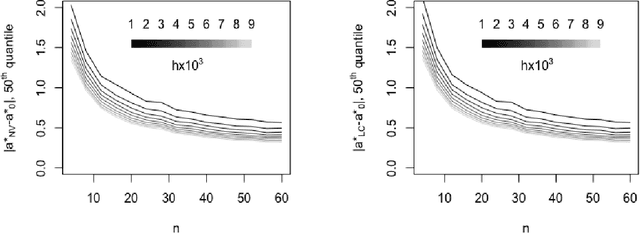
This paper establishes the asymptotic consistency of the {\it loss-calibrated variational Bayes} (LCVB) method. LCVB was proposed in~\cite{LaSiGh2011} as a method for approximately computing Bayesian posteriors in a `loss aware' manner. This methodology is also highly relevant in general data-driven decision-making contexts. Here, we not only establish the asymptotic consistency of the calibrated approximate posterior, but also the asymptotic consistency of decision rules. We also establish the asymptotic consistency of decision rules obtained from a `naive' variational Bayesian procedure.

Asymptotic Consistency of $α-$Rényi-Approximate Posteriors

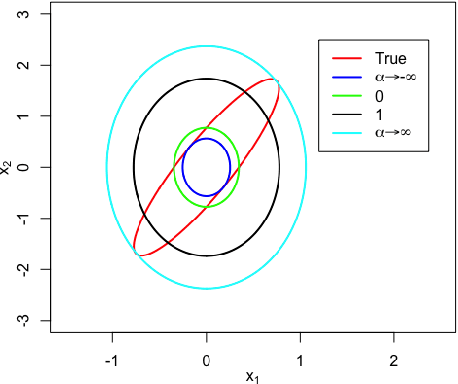
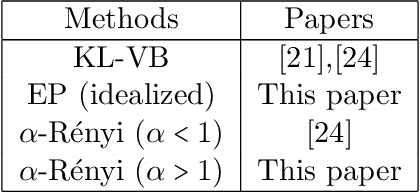
We study the asymptotic consistency properties of $\alpha$-R\'enyi approximate posteriors, a class of variational Bayesian methods that approximate an intractable Bayesian posterior with a member of a tractable family of distributions, the member chosen to minimize the $\alpha$-R\'enyi divergence from the true posterior. Unique to our work is that we consider settings with $\alpha > 1$, resulting in approximations that upperbound the log-likelihood, and consequently have wider spread than traditional variational approaches that minimize the Kullback-Liebler (KL) divergence from the posterior. Our primary result identifies sufficient conditions under which consistency holds, centering around the existence of a `good' sequence of distributions in the approximating family that possesses, among other properties, the right rate of convergence to a limit distribution. We also further characterize the good sequence by demonstrating that a sequence of distributions that converges too quickly cannot be a good sequence. We also illustrate the existence of good sequence with a number of examples. As an auxiliary result of our main theorems, we also recover the consistency of the idealized expectation propagation (EP) approximate posterior that minimizes the KL divergence from the posterior. Our results complement a growing body of work focused on the frequentist properties of variational Bayesian methods.