Distributed Robust Power System State Estimation

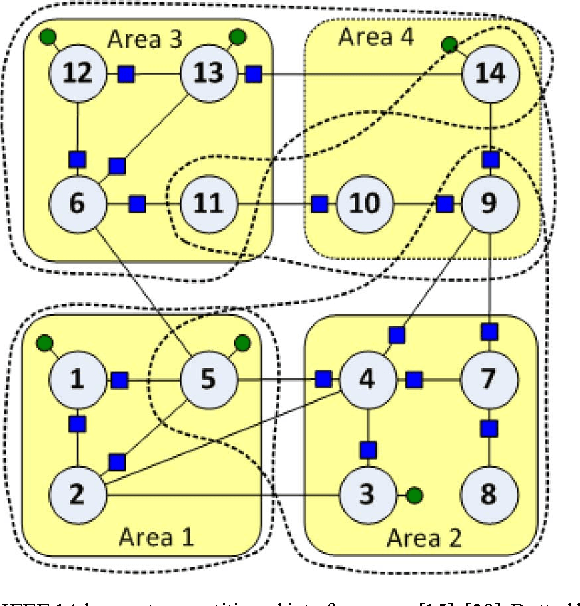
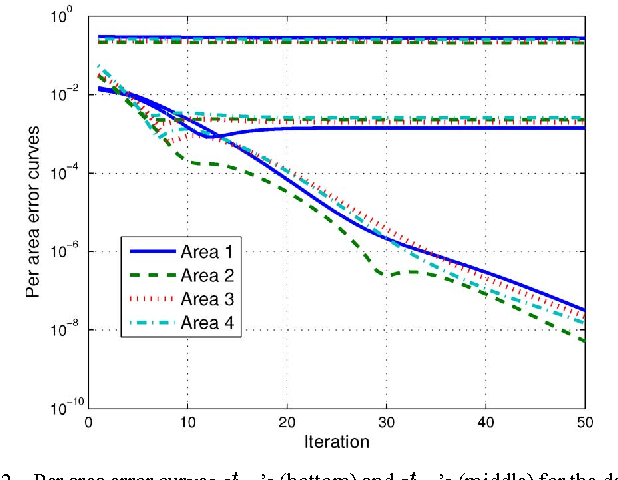
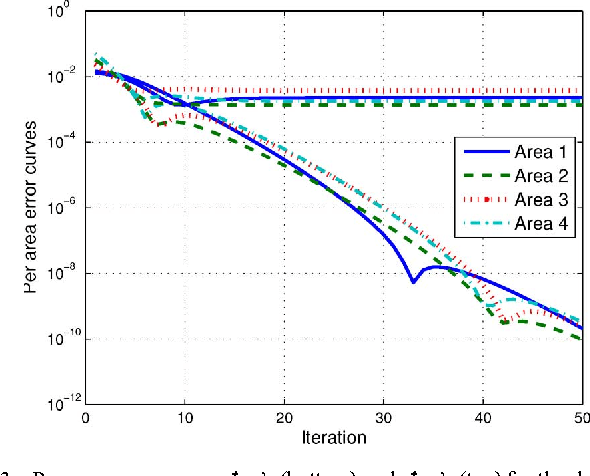
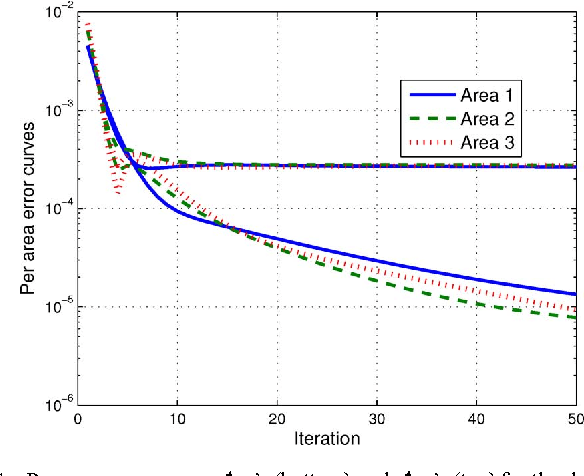
Deregulation of energy markets, penetration of renewables, advanced metering capabilities, and the urge for situational awareness, all call for system-wide power system state estimation (PSSE). Implementing a centralized estimator though is practically infeasible due to the complexity scale of an interconnection, the communication bottleneck in real-time monitoring, regional disclosure policies, and reliability issues. In this context, distributed PSSE methods are treated here under a unified and systematic framework. A novel algorithm is developed based on the alternating direction method of multipliers. It leverages existing PSSE solvers, respects privacy policies, exhibits low communication load, and its convergence to the centralized estimates is guaranteed even in the absence of local observability. Beyond the conventional least-squares based PSSE, the decentralized framework accommodates a robust state estimator. By exploiting interesting links to the compressive sampling advances, the latter jointly estimates the state and identifies corrupted measurements. The novel algorithms are numerically evaluated using the IEEE 14-, 118-bus, and a 4,200-bus benchmarks. Simulations demonstrate that the attainable accuracy can be reached within a few inter-area exchanges, while largest residual tests are outperformed.

Sparse Volterra and Polynomial Regression Models: Recoverability and Estimation

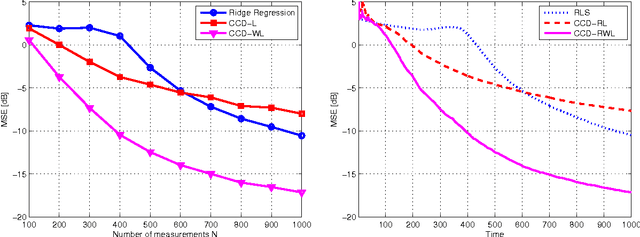
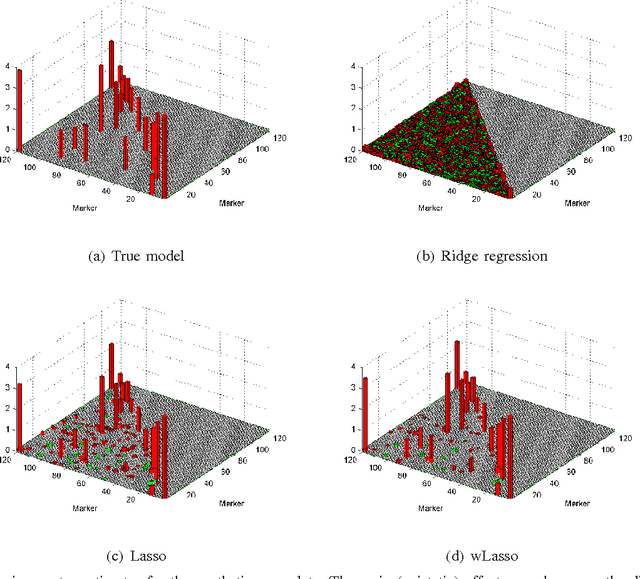
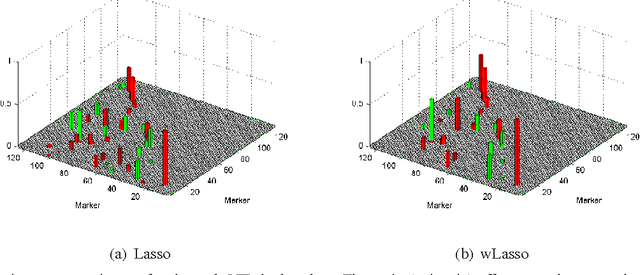
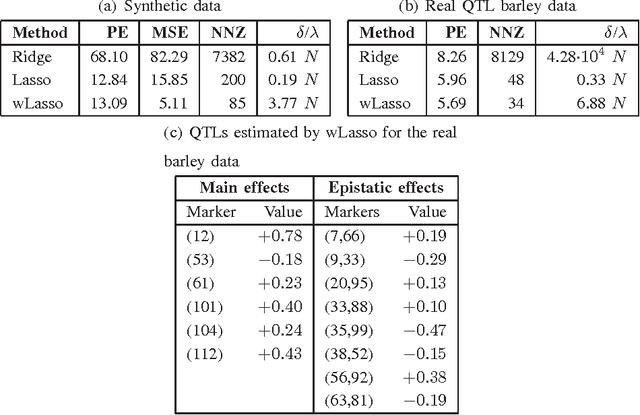
Volterra and polynomial regression models play a major role in nonlinear system identification and inference tasks. Exciting applications ranging from neuroscience to genome-wide association analysis build on these models with the additional requirement of parsimony. This requirement has high interpretative value, but unfortunately cannot be met by least-squares based or kernel regression methods. To this end, compressed sampling (CS) approaches, already successful in linear regression settings, can offer a viable alternative. The viability of CS for sparse Volterra and polynomial models is the core theme of this work. A common sparse regression task is initially posed for the two models. Building on (weighted) Lasso-based schemes, an adaptive RLS-type algorithm is developed for sparse polynomial regressions. The identifiability of polynomial models is critically challenged by dimensionality. However, following the CS principle, when these models are sparse, they could be recovered by far fewer measurements. To quantify the sufficient number of measurements for a given level of sparsity, restricted isometry properties (RIP) are investigated in commonly met polynomial regression settings, generalizing known results for their linear counterparts. The merits of the novel (weighted) adaptive CS algorithms to sparse polynomial modeling are verified through synthetic as well as real data tests for genotype-phenotype analysis.

Robust Clustering Using Outlier-Sparsity Regularization

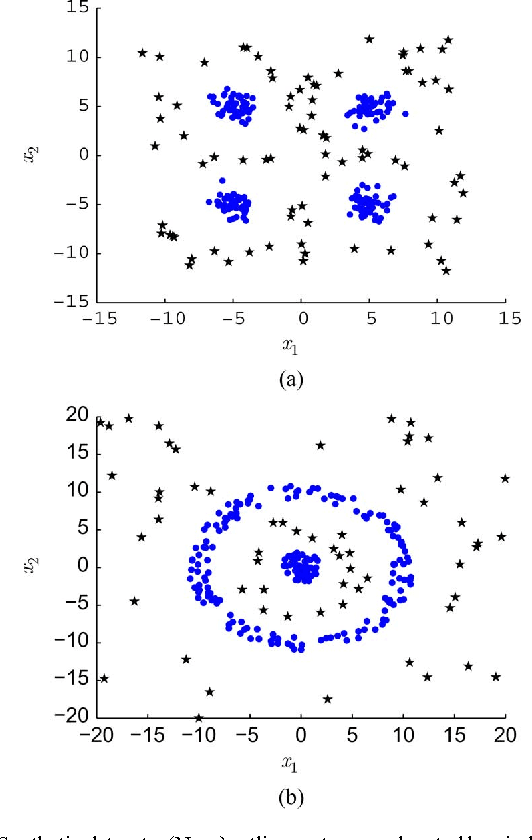
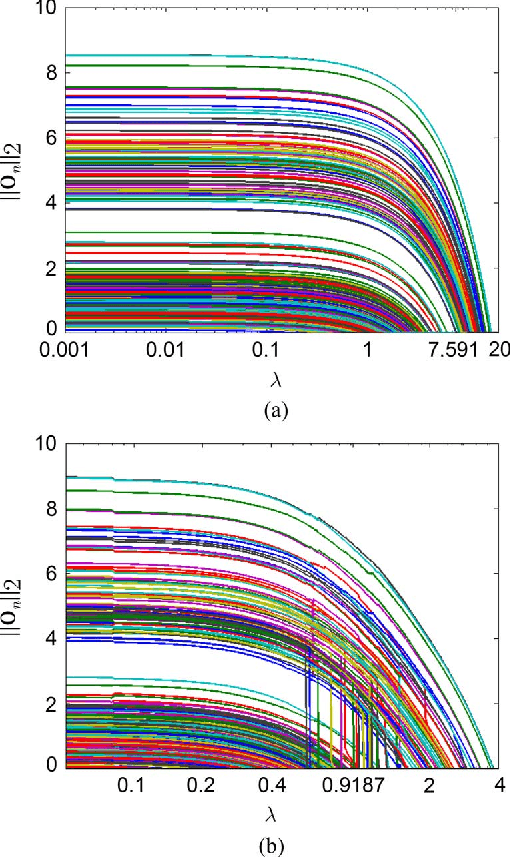
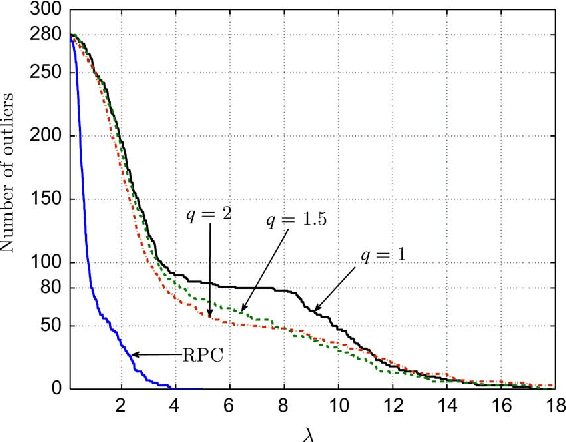
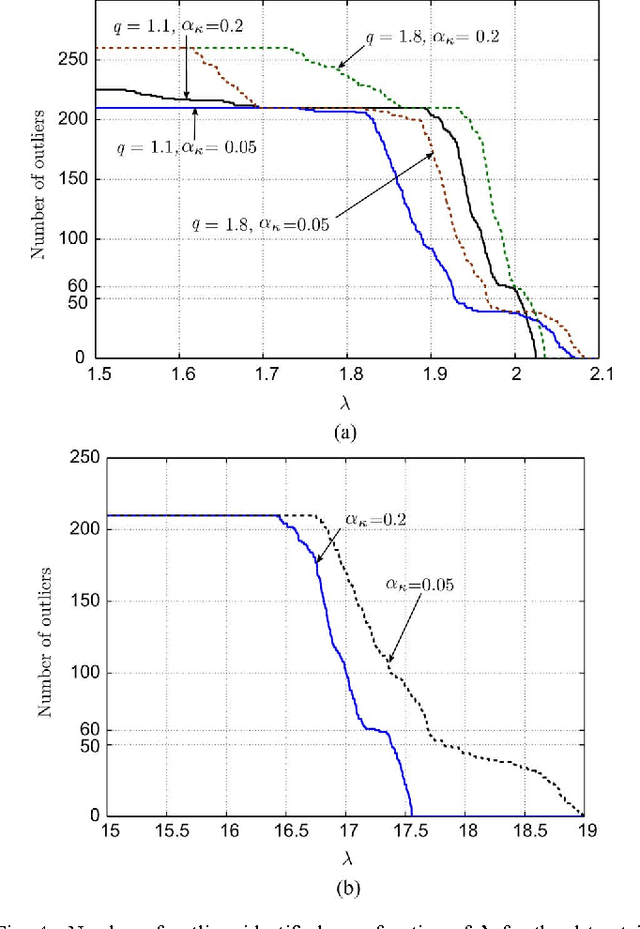
Notwithstanding the popularity of conventional clustering algorithms such as K-means and probabilistic clustering, their clustering results are sensitive to the presence of outliers in the data. Even a few outliers can compromise the ability of these algorithms to identify meaningful hidden structures rendering their outcome unreliable. This paper develops robust clustering algorithms that not only aim to cluster the data, but also to identify the outliers. The novel approaches rely on the infrequent presence of outliers in the data which translates to sparsity in a judiciously chosen domain. Capitalizing on the sparsity in the outlier domain, outlier-aware robust K-means and probabilistic clustering approaches are proposed. Their novelty lies on identifying outliers while effecting sparsity in the outlier domain through carefully chosen regularization. A block coordinate descent approach is developed to obtain iterative algorithms with convergence guarantees and small excess computational complexity with respect to their non-robust counterparts. Kernelized versions of the robust clustering algorithms are also developed to efficiently handle high-dimensional data, identify nonlinearly separable clusters, or even cluster objects that are not represented by vectors. Numerical tests on both synthetic and real datasets validate the performance and applicability of the novel algorithms.

From Sparse Signals to Sparse Residuals for Robust Sensing

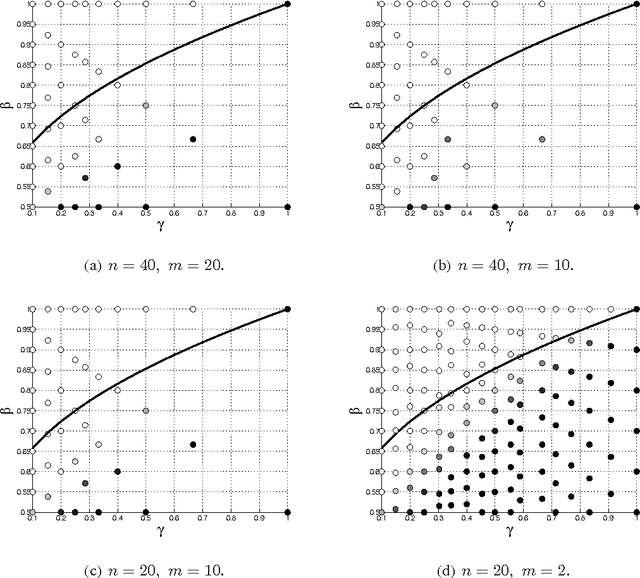
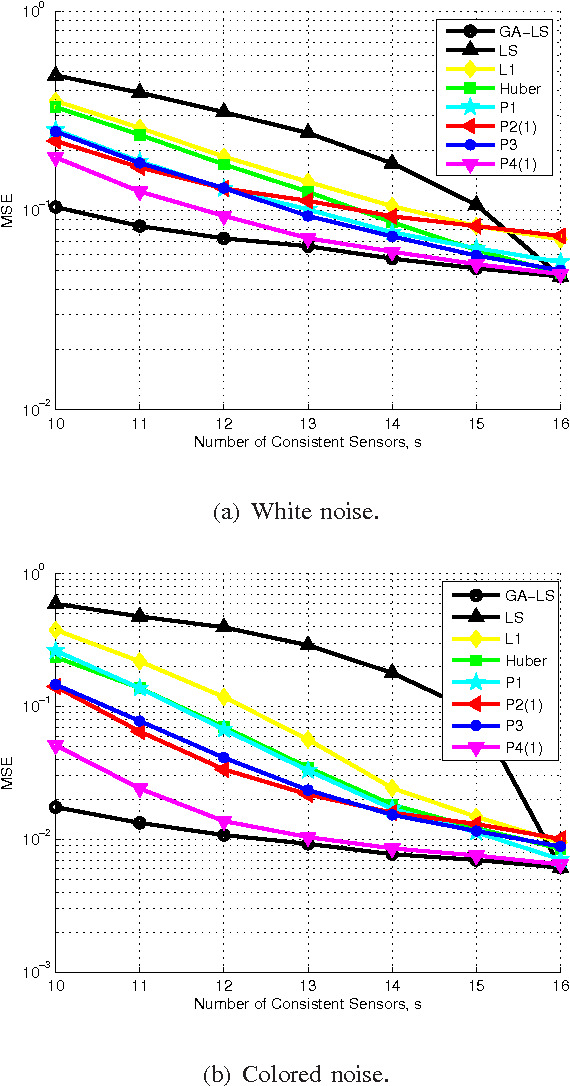
One of the key challenges in sensor networks is the extraction of information by fusing data from a multitude of distinct, but possibly unreliable sensors. Recovering information from the maximum number of dependable sensors while specifying the unreliable ones is critical for robust sensing. This sensing task is formulated here as that of finding the maximum number of feasible subsystems of linear equations, and proved to be NP-hard. Useful links are established with compressive sampling, which aims at recovering vectors that are sparse. In contrast, the signals here are not sparse, but give rise to sparse residuals. Capitalizing on this form of sparsity, four sensing schemes with complementary strengths are developed. The first scheme is a convex relaxation of the original problem expressed as a second-order cone program (SOCP). It is shown that when the involved sensing matrices are Gaussian and the reliable measurements are sufficiently many, the SOCP can recover the optimal solution with overwhelming probability. The second scheme is obtained by replacing the initial objective function with a concave one. The third and fourth schemes are tailored for noisy sensor data. The noisy case is cast as a combinatorial problem that is subsequently surrogated by a (weighted) SOCP. Interestingly, the derived cost functions fall into the framework of robust multivariate linear regression, while an efficient block-coordinate descent algorithm is developed for their minimization. The robust sensing capabilities of all schemes are verified by simulated tests.