Geometry of nonlinear forecast reconciliation

Forecast reconciliation, an ex-post technique applied to forecasts that must satisfy constraints, has been a prominent topic in the forecasting literature over the past two decades. Recently, several efforts have sought to extend reconciliation methods to the probabilistic settings. Nevertheless, formal theorems demonstrating error reduction in nonlinear contexts, analogous to those presented in Panagiotelis et al.(2021), are still lacking. This paper addresses that gap by establishing such theorems for various classes of nonlinear hypersurfaces and vector-valued functions. Specifically, we derive an exact analog of Theorem 3.1 from Panagiotelis et al.(2021) for hypersurfaces with constant-sign curvature. Additionally, we provide probabilistic guarantees for the broader case of hypersurfaces with non-constant-sign curvature and for general vector-valued functions. To support reproducibility and practical adoption, we release a JAX-based Python package, \emph{to be released upon publication}, implementing the presented theorems and reconciliation procedures.

Multivariate Boosted Trees and Applications to Forecasting and Control

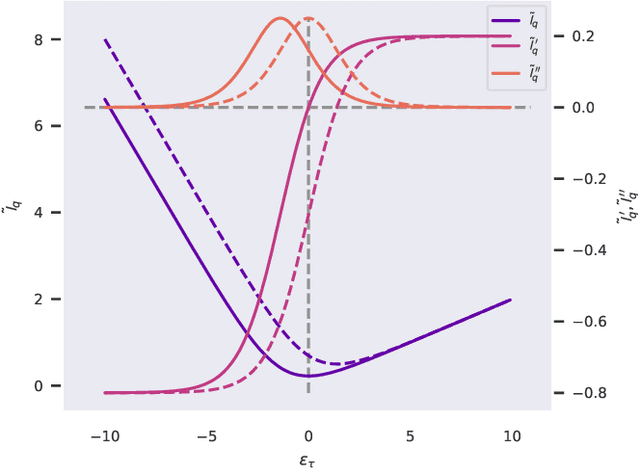
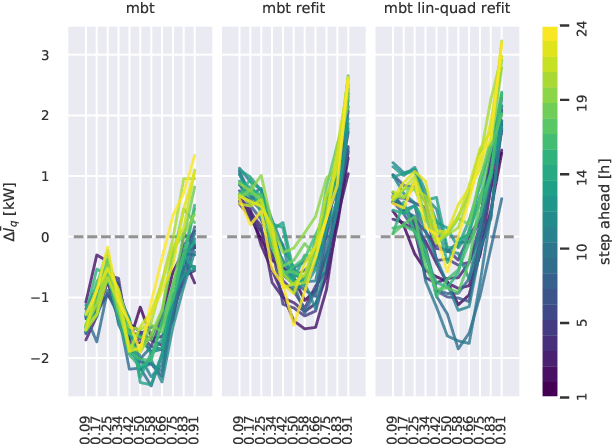
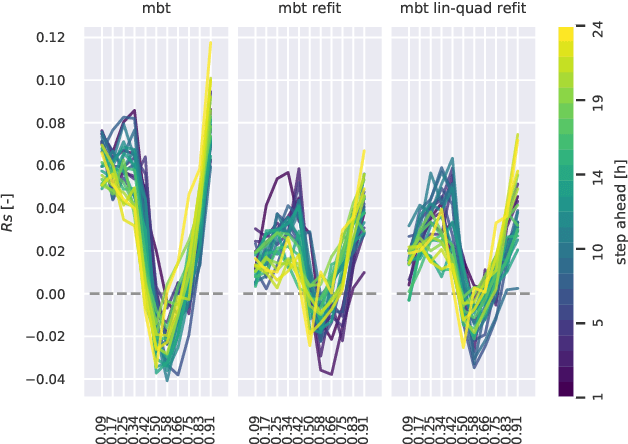
Gradient boosted trees are competition-winning, general-purpose, non-parametric regressors, which exploit sequential model fitting and gradient descent to minimize a specific loss function. The most popular implementations are tailored to univariate regression and classification tasks, precluding the possibility of capturing multivariate target cross-correlations and applying conditional penalties to the predictions. In this paper, we present a computationally efficient algorithm for fitting multivariate boosted trees. We show that multivariate trees can outperform their univariate counterpart when the predictions are correlated. Furthermore, the algorithm allows to arbitrarily regularize the predictions, so that properties like smoothness, consistency and functional relations can be enforced. We present applications and numerical results related to forecasting and control.

Hierarchical Demand Forecasting Benchmark for the Distribution Grid

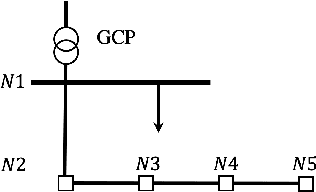
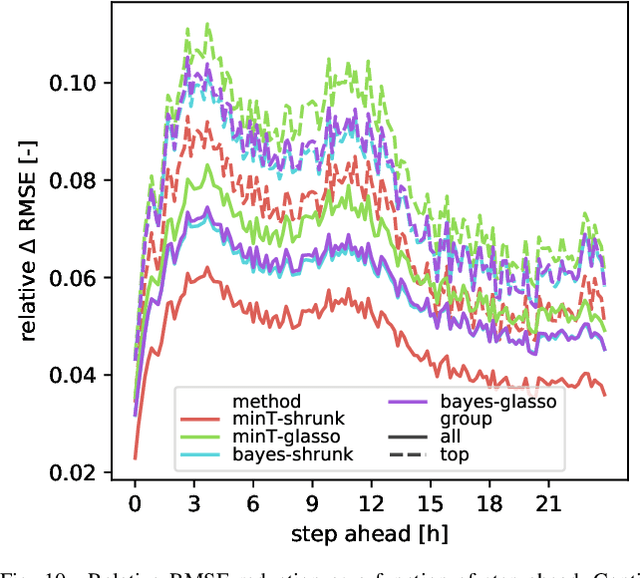
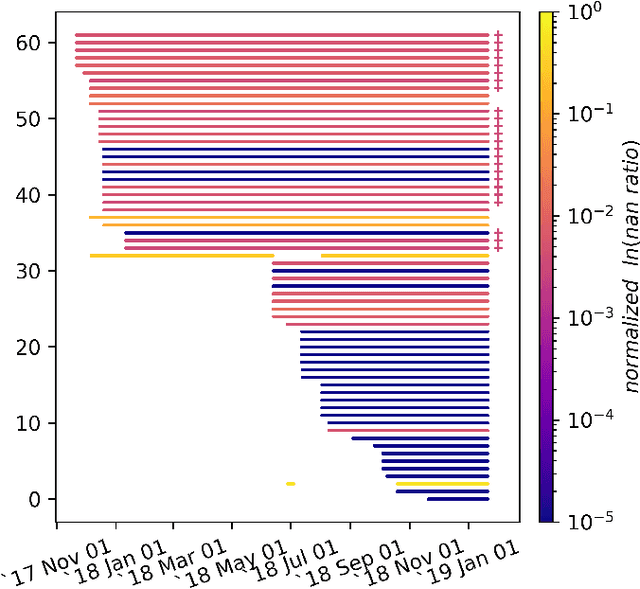
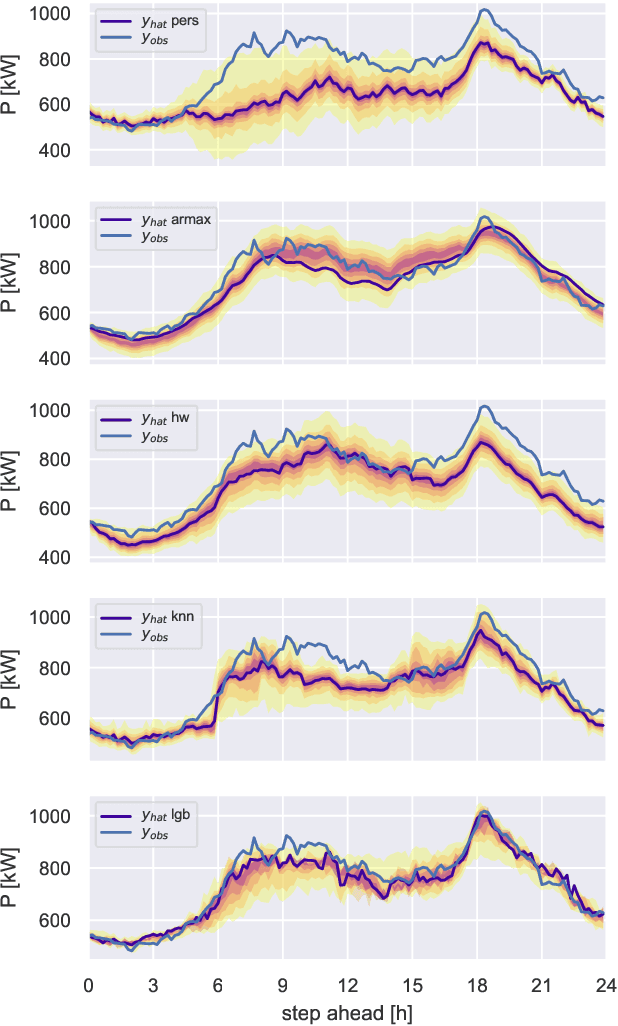
We present a comparative study of different probabilistic forecasting techniques on the task of predicting the electrical load of secondary substations and cabinets located in a low voltage distribution grid, as well as their aggregated power profile. The methods are evaluated using standard KPIs for deterministic and probabilistic forecasts. We also compare the ability of different hierarchical techniques in improving the bottom level forecasters' performances. Both the raw and cleaned datasets, including meteorological data, are made publicly available to provide a standard benchmark for evaluating forecasting algorithms for demand-side management applications.

An Unsupervised Method for Estimating the Global Horizontal Irradiance from Photovoltaic Power Measurements

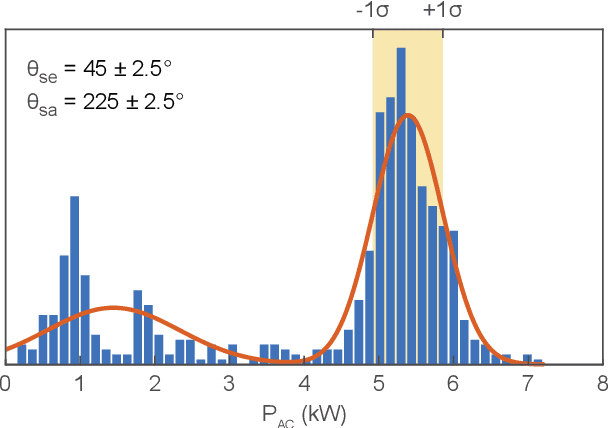
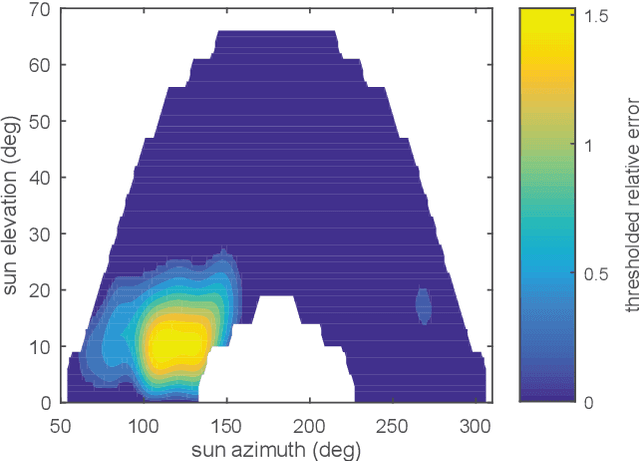
In this paper, we present a method to determine the global horizontal irradiance (GHI) from the power measurements of one or more PV systems, located in the same neighborhood. The method is completely unsupervised and is based on a physical model of a PV plant. The precise assessment of solar irradiance is pivotal for the forecast of the electric power generated by photovoltaic (PV) plants. However, on-ground measurements are expensive and are generally not performed for small and medium-sized PV plants. Satellite-based services represent a valid alternative to on site measurements, but their space-time resolution is limited. Results from two case studies located in Switzerland are presented. The performance of the proposed method at assessing GHI is compared with that of free and commercial satellite services. Our results show that the presented method is generally better than satellite-based services, especially at high temporal resolutions.