Deficiency of equation-finding approach to data-driven modeling of dynamical systems

Finding the governing equations from data by sparse optimization has become a popular approach to deterministic modeling of dynamical systems. Considering the physical situations where the data can be imperfect due to disturbances and measurement errors, we show that for many chaotic systems, widely used sparse-optimization methods for discovering governing equations produce models that depend sensitively on the measurement procedure, yet all such models generate virtually identical chaotic attractors, leading to a striking limitation that challenges the conventional notion of equation-based modeling in complex dynamical systems. Calculating the Koopman spectra, we find that the different sets of equations agree in their large eigenvalues and the differences begin to appear when the eigenvalues are smaller than an equation-dependent threshold. The results suggest that finding the governing equations of the system and attempting to interpret them physically may lead to misleading conclusions. It would be more useful to work directly with the available data using, e.g., machine-learning methods.

Dynamical Landscape and Multistability of the Earth's Climate

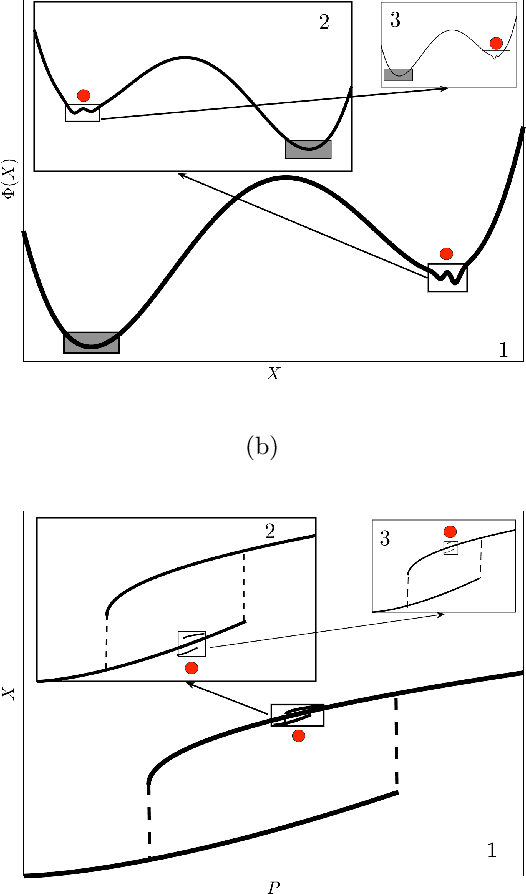
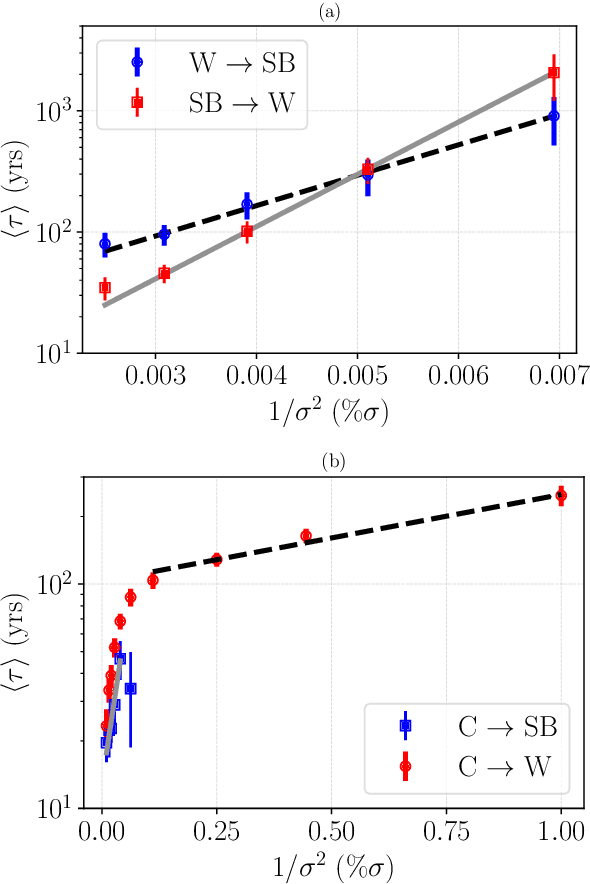
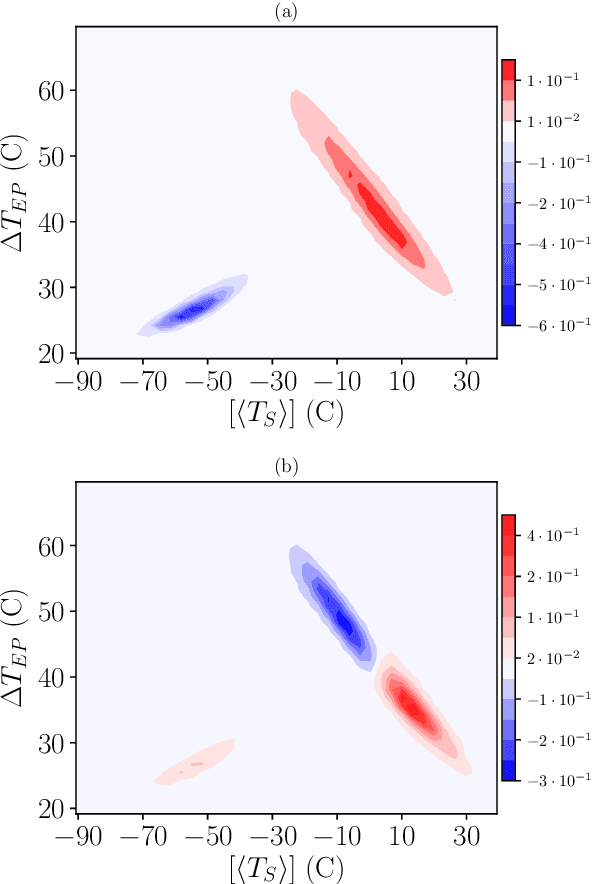
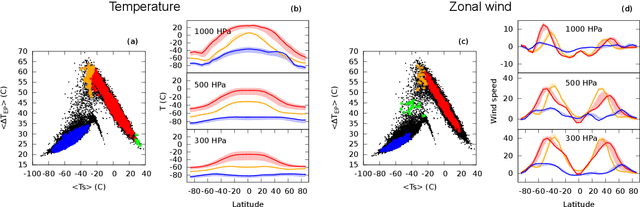
We apply two independent data analysis methodologies to locate stable climate states in an intermediate complexity climate model. First, drawing from the theory of quasipotentials, and viewing the state space as an energy landscape with valleys and mountain ridges, we infer the relative likelihood of the identified multistable climate states, and investigate the most likely transition trajectories as well as the expected transition times between them. Second, harnessing techniques from data science, specifically manifold learning, we characterize the data landscape of the simulation data to find climate states and basin boundaries within a fully agnostic and unsupervised framework. Both approaches show remarkable agreement, and reveal, apart from the well known warm and snowball earth states, a third intermediate stable state in one of the two climate models we consider. The combination of our approaches allows to identify how the negative feedback of ocean heat transport and entropy production via the hydrological cycle drastically change the topography of the dynamical landscape of Earth's climate.