STaR-Bets: Sequential Target-Recalculating Bets for Tighter Confidence Intervals

The construction of confidence intervals for the mean of a bounded random variable is a classical problem in statistics with numerous applications in machine learning and virtually all scientific fields. In particular, obtaining the tightest possible confidence intervals is vital every time the sampling of the random variables is expensive. The current state-of-the-art method to construct confidence intervals is by using betting algorithms. This is a very successful approach for deriving optimal confidence sequences, even matching the rate of law of iterated logarithms. However, in the fixed horizon setting, these approaches are either sub-optimal or based on heuristic solutions with strong empirical performance but without a finite-time guarantee. Hence, no betting-based algorithm guaranteeing the optimal $\mathcal{O}(\sqrt{\frac{\sigma^2\log\frac1\delta}{n}})$ width of the confidence intervals are known. This work bridges this gap. We propose a betting-based algorithm to compute confidence intervals that empirically outperforms the competitors. Our betting strategy uses the optimal strategy in every step (in a certain sense), whereas the standard betting methods choose a constant strategy in advance. Leveraging this fact results in strict improvements even for classical concentration inequalities, such as the ones of Hoeffding or Bernstein. Moreover, we also prove that the width of our confidence intervals is optimal up to an $1+o(1)$ factor diminishing with $n$. The code is available on~https://github.com/vvoracek/STaR-bets-confidence-interval.

Sound Randomized Smoothing in Floating-Point Arithmetics

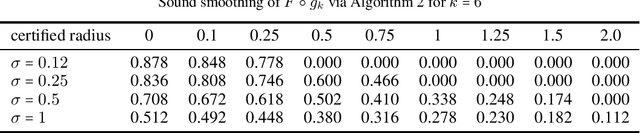
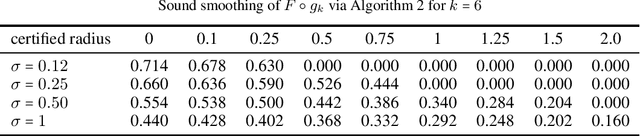
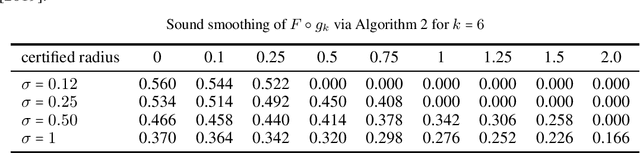
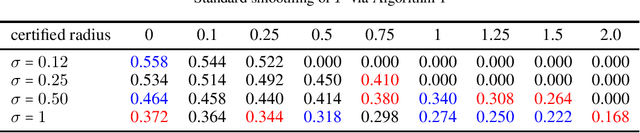
Randomized smoothing is sound when using infinite precision. However, we show that randomized smoothing is no longer sound for limited floating-point precision. We present a simple example where randomized smoothing certifies a radius of $1.26$ around a point, even though there is an adversarial example in the distance $0.8$ and extend this example further to provide false certificates for CIFAR10. We discuss the implicit assumptions of randomized smoothing and show that they do not apply to generic image classification models whose smoothed versions are commonly certified. In order to overcome this problem, we propose a sound approach to randomized smoothing when using floating-point precision with essentially equal speed and matching the certificates of the standard, unsound practice for standard classifiers tested so far. Our only assumption is that we have access to a fair coin.

Provably Adversarially Robust Nearest Prototype Classifiers

Nearest prototype classifiers (NPCs) assign to each input point the label of the nearest prototype with respect to a chosen distance metric. A direct advantage of NPCs is that the decisions are interpretable. Previous work could provide lower bounds on the minimal adversarial perturbation in the $\ell_p$-threat model when using the same $\ell_p$-distance for the NPCs. In this paper we provide a complete discussion on the complexity when using $\ell_p$-distances for decision and $\ell_q$-threat models for certification for $p,q \in \{1,2,\infty\}$. In particular we provide scalable algorithms for the \emph{exact} computation of the minimal adversarial perturbation when using $\ell_2$-distance and improved lower bounds in other cases. Using efficient improved lower bounds we train our Provably adversarially robust NPC (PNPC), for MNIST which have better $\ell_2$-robustness guarantees than neural networks. Additionally, we show up to our knowledge the first certification results w.r.t. to the LPIPS perceptual metric which has been argued to be a more realistic threat model for image classification than $\ell_p$-balls. Our PNPC has on CIFAR10 higher certified robust accuracy than the empirical robust accuracy reported in (Laidlaw et al., 2021). The code is available in our repository.